题目内容
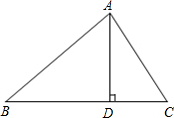 如图,在△ABC中,AD是BC上的高,tan∠B=cos∠DAC,若sinC=
如图,在△ABC中,AD是BC上的高,tan∠B=cos∠DAC,若sinC=| 12 |
| 13 |
考点:解直角三角形
专题:
分析:根据sinC=
=
设AD=12x,AC=13x,由勾股定理求出DC=5x,根据cos∠DAC=
=
,tan∠B=
=
,求出BD=13x,得出方程13x+5x=36,求出x即可.
| 12 |
| 13 |
| AD |
| AC |
| AD |
| AC |
| 12 |
| 13 |
| AD |
| BD |
| 12x |
| BD |
解答:解:∵AD是BC上的高,
∴∠ADB=∠ADC=90°,
∵sinC=
=
,
设AD=12x,AC=13x,由勾股定理得:DC=5x,
∵tan∠B=cos∠DAC=
=
,tan∠B=
=
,
∴BD=13x,
∵BC=BD+DC=13x+5x=36,
∴x=2,
∴AD=12x=24.
∴∠ADB=∠ADC=90°,
∵sinC=
| 12 |
| 13 |
| AD |
| AC |
设AD=12x,AC=13x,由勾股定理得:DC=5x,
∵tan∠B=cos∠DAC=
| AD |
| AC |
| 12 |
| 13 |
| AD |
| BD |
| 12x |
| BD |
∴BD=13x,
∵BC=BD+DC=13x+5x=36,
∴x=2,
∴AD=12x=24.
点评:本题考查了解直角三角形的应用,主要考查学生的计算能力,题目比较好,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
把抛物线y=x2-2x-4先向上平移2个单位,再向右平移3个单位,所得的抛物线是( )
| A、y=x2-8x+10 |
| B、y=x2+8x-10 |
| C、y=x2-8x+13 |
| D、y=x2+8x+13 |
如果直线MN平行于x轴,那么点M,N的坐标之间的关系是( )
| A、横坐标相等 |
| B、纵坐标相等 |
| C、横坐标的绝对值相等 |
| D、纵坐标互为相反数 |
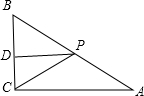 如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,点P是AB上的一个动点(不与点B重合),PD⊥BC,垂足为D,设PD的长为x,△PBC的面积为y.
如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,点P是AB上的一个动点(不与点B重合),PD⊥BC,垂足为D,设PD的长为x,△PBC的面积为y. 如图,已知抛物线y=-x2+6x-5.
如图,已知抛物线y=-x2+6x-5.