题目内容
 如图,已知抛物线y=-x2+6x-5.
如图,已知抛物线y=-x2+6x-5.(1)若抛物线y=ax2+bx+c与y=-x2+6x-5关于原点O中心对称,求此抛物线的解析式;
(2)根据(1)的解题结果,合理猜想:直接写出抛物线y=a(x-m)2+n关于原点O中心对称的二次函数解析式(不要求写推导过程);
(3)若(1)中抛物线y=ax2+bx+c与y轴交于点M,与x轴交于点A和点B(点A在左),点C是线段AB的中点,求sin∠CMA;
(4)在(3)的条件下,在抛物线y=ax2+bx+c上是否存在点P,使△OPA的面积与△MCA的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)根据中心对称即可求得y=ax2+bx+c中a,b,c的值;
(2)根据(1)中,y=-x2+6x-5关于原点O中心对称的解析式为y=x2+6x+5,可得抛物线y=a(x-m)2+n关于原点O中心对称的二次函数解析式为y=-a(x+m)2-n;
(3)过C作CG⊥AM,可以求得CG的值,根据CG和CM的值即可解题;
(4)根据题意可知只要P点到x轴的距离为
即可,取y=±
即可求得相应的P点.
(2)根据(1)中,y=-x2+6x-5关于原点O中心对称的解析式为y=x2+6x+5,可得抛物线y=a(x-m)2+n关于原点O中心对称的二次函数解析式为y=-a(x+m)2-n;
(3)过C作CG⊥AM,可以求得CG的值,根据CG和CM的值即可解题;
(4)根据题意可知只要P点到x轴的距离为
| 8 |
| 5 |
| 8 |
| 5 |
解答:解:(1)y=-x2+6x-5顶点为(3,4)与x交点为(1,0),(5,0)
抛物线y=ax2+bx+c与y=-x2+6x-5关于原点O中心对称,
∴抛物线y=ax2+bx+c经过(-3,-4)(-5,0),(-1,0)
∴抛物线y=ax2+bx+c=x2+6x+5;
(2)y=-a(x+m)2-n;
(3)过C作CG⊥AM,
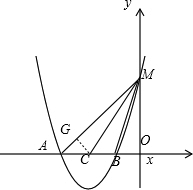
y=x2+6x+5交x轴与A,B点,C为AB中点,
∴A(-5,0),B(-1,0),C(-3,0),M(0,4)
∴AM=
,CM=5,
根据三角形面积相等可得CG•AM=AC•OM,CG=
,
∴求sin∠CMA=
=
;
(4)∵△MCA的面积=
AC•OM=4,
∴△OPA的面积与△MCA的面积相等,即P点到x轴距离为为
=
即可,
y=x2+6x+5=
或y=x2+6x+5=-
,
解得x=
或
时成立,
故P点坐标可以为(
,
),(
,
),(
,-
),(
,-
).
抛物线y=ax2+bx+c与y=-x2+6x-5关于原点O中心对称,
∴抛物线y=ax2+bx+c经过(-3,-4)(-5,0),(-1,0)
∴抛物线y=ax2+bx+c=x2+6x+5;
(2)y=-a(x+m)2-n;
(3)过C作CG⊥AM,

y=x2+6x+5交x轴与A,B点,C为AB中点,
∴A(-5,0),B(-1,0),C(-3,0),M(0,4)
∴AM=
| 41 |
根据三角形面积相等可得CG•AM=AC•OM,CG=
| 8 | ||
|
∴求sin∠CMA=
| CG |
| CM |
| 8 | ||
5
|
(4)∵△MCA的面积=
| 1 |
| 2 |
∴△OPA的面积与△MCA的面积相等,即P点到x轴距离为为
| 2×4 |
| 5 |
| 8 |
| 5 |
y=x2+6x+5=
| 8 |
| 5 |
| 8 |
| 5 |
解得x=
-15±
| ||
| 5 |
-15±2
| ||
| 5 |
故P点坐标可以为(
-15+
| ||
| 5 |
| 8 |
| 5 |
-15-
| ||
| 5 |
| 8 |
| 5 |
-15+2
| ||
| 5 |
| 8 |
| 5 |
-15-2
| ||
| 5 |
| 8 |
| 5 |
点评:本题考查了中心对称性质,考查了二次函数解析式的求解,考查了三角形内角正弦值的计算,考查了二次函数的运用.

练习册系列答案
相关题目
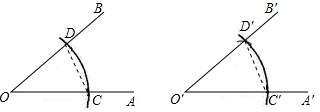 请仔细观察用直尺和圆规作一个角等于已知角的示意图,请你根据所学的三角形全等有关的知识,说明画出∠A′O′B′=∠AOB的依据是( )
请仔细观察用直尺和圆规作一个角等于已知角的示意图,请你根据所学的三角形全等有关的知识,说明画出∠A′O′B′=∠AOB的依据是( )| A、SAS | B、ASA |
| C、AAS | D、SSS |
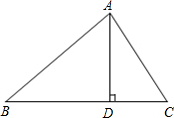 如图,在△ABC中,AD是BC上的高,tan∠B=cos∠DAC,若sinC=
如图,在△ABC中,AD是BC上的高,tan∠B=cos∠DAC,若sinC= 水坝横截面为等腰梯形,尺寸如图,(单位:米)坡度I=
水坝横截面为等腰梯形,尺寸如图,(单位:米)坡度I=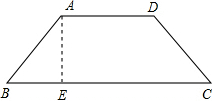 如图,铁路路基的横截面是等腰梯形,斜坡AB的坡度为1:
如图,铁路路基的横截面是等腰梯形,斜坡AB的坡度为1: