题目内容
把抛物线y=x2-2x-4先向上平移2个单位,再向右平移3个单位,所得的抛物线是( )
| A、y=x2-8x+10 |
| B、y=x2+8x-10 |
| C、y=x2-8x+13 |
| D、y=x2+8x+13 |
考点:二次函数图象与几何变换
专题:
分析:直接根据二次函数图象平移的法则即可得出结论.
解答:解:∵y=x2-2x-4=(x-1)2-5,
∴根据“上加下减,左加右减”的法则可知,将抛物线y=(x-1)2-5先向上平移2个单位,再向右平移3个单位,所得的抛物线是:y=(x-1-3)2-5+2=x2-8x+13,即
y=x2-8x+13.
故选:C.
∴根据“上加下减,左加右减”的法则可知,将抛物线y=(x-1)2-5先向上平移2个单位,再向右平移3个单位,所得的抛物线是:y=(x-1-3)2-5+2=x2-8x+13,即
y=x2-8x+13.
故选:C.
点评:本题考查的是二次函数的图象与几何变换,先把原抛物线的解析式化为顶点式的形式是解答此题的关键.

练习册系列答案
相关题目
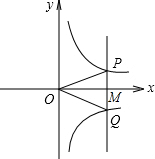 如图,若点M是x轴正半轴上任意一点,过点M作PQ∥y轴,分别交函数y=
如图,若点M是x轴正半轴上任意一点,过点M作PQ∥y轴,分别交函数y=| k1 |
| x |
| k2 |
| x |
①∠POQ可能等于90°;②
| PM |
| MQ |
| K1 |
| K2 |
| 1 |
| 2 |
其中一定正确的是( )
| A、①② | B、②③ | C、①③ | D、①④ |
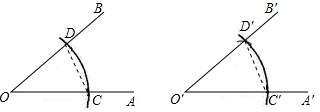 请仔细观察用直尺和圆规作一个角等于已知角的示意图,请你根据所学的三角形全等有关的知识,说明画出∠A′O′B′=∠AOB的依据是( )
请仔细观察用直尺和圆规作一个角等于已知角的示意图,请你根据所学的三角形全等有关的知识,说明画出∠A′O′B′=∠AOB的依据是( )| A、SAS | B、ASA |
| C、AAS | D、SSS |
 如图,在正方形ABCD内有一折线段,其中,AE⊥EF,EF⊥FC,并且AE=4,EF=3,FC=5,则该正方形的边长为
如图,在正方形ABCD内有一折线段,其中,AE⊥EF,EF⊥FC,并且AE=4,EF=3,FC=5,则该正方形的边长为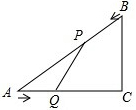 已知,如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s,点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s,连接PQ,若设运动的时间为t(s)(0<t<2),解答下列问题:
已知,如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s,点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s,连接PQ,若设运动的时间为t(s)(0<t<2),解答下列问题: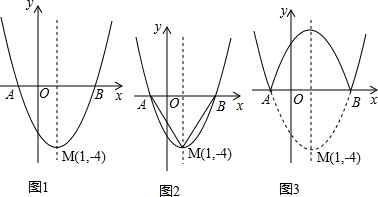
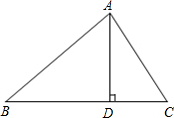 如图,在△ABC中,AD是BC上的高,tan∠B=cos∠DAC,若sinC=
如图,在△ABC中,AD是BC上的高,tan∠B=cos∠DAC,若sinC=