题目内容

15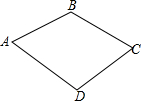．如图，在四边形ABCD中，点D在线段AB、BC的垂直平分线上，若∠D=110°，则∠B度数为（　　）
A．110°B．115°C．120°D．125°

分析 连接BD，根据线段的垂直平分线性质得出BD=AD，DC=BD，推出∠A=∠ABD，∠C=∠CBD，求出∠ABC=∠ABD+∠CBD=∠A+∠C，再根据四边形的内角和定理即可求出答案．

解答 解：连接BD，
∵点D在线段AB、BC的垂直平分线上，
∴BD=AD，DC=BD，
∴∠A=∠ABD，∠C=∠CBD，
∴∠ABC=∠ABD+∠CBD=∠A+∠C，
∴∠ABC=（360°-∠D）÷2=125°．
故选：D．

点评 本题考查了四边形的内角和定理，等腰三角形的性质和判定，线段垂直平分线性质的应用，注意：线段垂直平分线上的点到线段两个端点的距离相等．

练习册系列答案
相关题目
5．约分：$\frac{{4{m^2}（{m-1}）}}{{6mn（{1-m}）}}$．
6．先阅读，再回答问题：要比较代数式A、B的大小，可以作差A-B，比较差的取值，当A-B＞0时，有A＞B；当A-B=0时，有A=B；当A-B＜0时，有A＜B．”例如，当a＜0时，比较a2和a（a+1）的大小．可以观察a2-a（a+1）=a2-a2-a=-a．因为当a＜0时，-a＞0，所以当a＜0时，a2＞a（a+1）．
（1）已知M=（x-2）（x-16），N=（x-4）（x-8），比较M、N的大小关系．
（2）某种产品的原料提价，因而厂家决定对于产品进行提价，现有三种方案：
方案1：第一次提价p%，第二次提价q%；
方案2：第一次提价q%，第二次提价p%；
方案3：第一、二次提价均为$\frac{p+q}{2}$%．
如果设原价为a元，请用含a、p、q的式子表示提价后三种方案的价格．
方案1：a（1+p%）（1+q%）；方案2：a（1+p%）（1+q%）；方案3：a（1+$\frac{p+q}{2}$%）2
?如果p，q是不相等的正数，三种方案哪种提价最多？
3．小明和小亮在玩摸球游戏，在一个盒子里装有除颜色外其他均相同的2个红球和3个白球，现从中任取2个球，则取到的是一个红球，一个白球的概率为（　　）
A．$\frac{2}{5}$B．$\frac{2}{3}$C．$\frac{3}{5}$D．$\frac{3}{10}$
10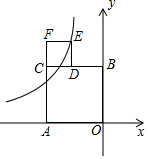．如图，四边形AOBC和四边形CDEF都是正方形，边OA在x轴上，边OB在y轴上，点D在边CB上，反比例函数y=$-\frac{8}{x}$在第二象限的图象经过点E，则正方形AOBC和正方形CDEF的面积之差为（　　）
A．12B．10C．8D．6
20．2022年将在北京--张家口举办冬季奥运会，北京将成为世界上第一个既举办夏季奥运会，又举办冬季奥运会的城市，某校开设了冰球选修课，12名同学被分成甲、乙两组进行训练，他们的身高（单位：cm）如表所示：
队员1队员2队员3队员4队员5队员6
甲组176177175176177175
乙组178175170174183176
设两队队员身高的平均数依次为$\overline{x}$甲，$\overline{x}$乙，方差依次为S甲2，S乙2，下列关系中正确的是（　　）
A．$\overline{x}$甲=$\overline{x}$乙，S甲2＜S乙2B．$\overline{x}$甲=$\overline{x}$乙，S甲2＞S乙2
C．$\overline{x}$甲＜$\overline{x}$乙，S甲2＜S乙2D．$\overline{x}$甲＞$\overline{x}$乙，S甲2＞S乙2
7．如图，数轴上的四个点A，B，C，D对应的数为整数，且AB=BC=CD=1，若|a|+|b|=2，则原点的位置可能是（　　）
A．A或BB．B或CC．C或DD．D或A
4．一个不透明的袋子中装有仅颜色不同的2个红球和2个白球，两个人依次从袋子中随机摸出一个小球不放回，则第一个人摸到红球且第二个人摸到白球的概率是（　　）
A．$\frac{1}{3}$B．$\frac{1}{2}$C．$\frac{1}{4}$D．$\frac{1}{6}$
5．下列计算正确的是（　　）
A．（3xy2）3=9x3y6B．B、（x+y）2=x2+y2
C．x6÷x2=x3D．2x2y-$\frac{1}{2}$yx2=$\frac{3}{2}$x2y

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网