题目内容
17.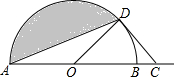 如图,AB为半圆O的直径,AB=4,C为AB延长线上一点,BC=2$\sqrt{2}$-2,过点作半圆的切线,切点为D,连接AD,则阴影部分的面积为$\frac{3}{2}$π-$\sqrt{2}$.
如图,AB为半圆O的直径,AB=4,C为AB延长线上一点,BC=2$\sqrt{2}$-2,过点作半圆的切线,切点为D,连接AD,则阴影部分的面积为$\frac{3}{2}$π-$\sqrt{2}$.
分析 首先求出∠AOD的度数,根据S阴=S扇形OAD-S△AOD计算即可.
解答 解:作DH⊥AB于H.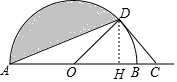
∵CD是⊙O的切线,
∴OD⊥CD,
∴∠ODC=90°,
∵OD=2,OC=OB+BC=2$\sqrt{2}$,
∴cos∠DOC=$\frac{OD}{OC}$=$\frac{\sqrt{2}}{2}$,
∴∠DOC=45°,DH=2×sin45°=2×$\frac{\sqrt{2}}{2}$,
∴∠AOD=135°,
∴S阴=S扇形OAD-S△AOD=$\frac{135•π•{2}^{2}}{360}$-$\frac{1}{2}$•2•2•$\frac{\sqrt{2}}{2}$=$\frac{3}{2}$π-$\sqrt{2}$.
故答案为$\frac{3}{2}$π-$\sqrt{2}$.
点评 本题考查切线的性质、扇形的面积的计算、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
7.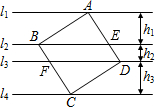 如图,正方形ABCD的四个顶点分别在四条平行线l1、l2、l3、l4上,这四条直线中相邻两条之间的距离依次为h1、h2、h3.若h1=2,h2=1,则正方形ABCD的面积为( )
如图,正方形ABCD的四个顶点分别在四条平行线l1、l2、l3、l4上,这四条直线中相邻两条之间的距离依次为h1、h2、h3.若h1=2,h2=1,则正方形ABCD的面积为( )
 如图,正方形ABCD的四个顶点分别在四条平行线l1、l2、l3、l4上,这四条直线中相邻两条之间的距离依次为h1、h2、h3.若h1=2,h2=1,则正方形ABCD的面积为( )
如图,正方形ABCD的四个顶点分别在四条平行线l1、l2、l3、l4上,这四条直线中相邻两条之间的距离依次为h1、h2、h3.若h1=2,h2=1,则正方形ABCD的面积为( )| A. | 9 | B. | 10 | C. | 13 | D. | 25 |
8. 如图为某商店的宣传单,小胜到此店同时购买了一件标价为x元的衣服和一条标价为y元的裤子,共节省500元,则根据题意所列方程正确的是( )
如图为某商店的宣传单,小胜到此店同时购买了一件标价为x元的衣服和一条标价为y元的裤子,共节省500元,则根据题意所列方程正确的是( )
 如图为某商店的宣传单,小胜到此店同时购买了一件标价为x元的衣服和一条标价为y元的裤子,共节省500元,则根据题意所列方程正确的是( )
如图为某商店的宣传单,小胜到此店同时购买了一件标价为x元的衣服和一条标价为y元的裤子,共节省500元,则根据题意所列方程正确的是( )| A. | 0.6x+0.4y+100=500 | B. | 0.6x+0.4y-100=500 | ||
| C. | 0.4x+0.6y+100=500 | D. | 0.4x+0.6y-100=500 |
5.估计2$\sqrt{13}$-1的值介于( )
| A. | 4和5之间 | B. | 5和6之间 | C. | 6和7之间 | D. | 7和8之间 |
12.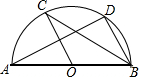 如图,AB是⊙O的直径,C、D是⊙O上的点,且OC∥BD,∠A=30°,则∠CBD=( )
如图,AB是⊙O的直径,C、D是⊙O上的点,且OC∥BD,∠A=30°,则∠CBD=( )
 如图,AB是⊙O的直径,C、D是⊙O上的点,且OC∥BD,∠A=30°,则∠CBD=( )
如图,AB是⊙O的直径,C、D是⊙O上的点,且OC∥BD,∠A=30°,则∠CBD=( )| A. | 10° | B. | 15° | C. | 30° | D. | 45° |
2.在下列正多边形瓷砖中,如果仅用一种正多变形瓷砖铺地面,那么不能将地面密铺的是( )
| A. | 正三角形 | B. | 正四边形 | C. | 正五边形 | D. | 正六边形 |
9.(-$\frac{1}{3}$)0=( )
| A. | 1 | B. | 0 | C. | -$\frac{1}{3}$ | D. | -3 |
 如图,在△ABC中,∠ACB=90°,AC=2.8,BC=2.1,则高CD=1.68.
如图,在△ABC中,∠ACB=90°,AC=2.8,BC=2.1,则高CD=1.68.