题目内容
7.已知点A(a,b)在双曲线y=$\frac{5}{x}$上,若a、b都是正整数,则图象经过B(a,0)、C(0,b)两点的一次函数的解析式(也称关系式)为y=-5x+5或y=-$\frac{1}{5}$x+1.分析 先根据反比例函数图象上点的坐标特征得出ab=5,由a、b都是正整数,得到a=1,b=5或a=5,b=1.再分两种情况进行讨论:当a=1,b=5;②a=5,b=1,利用待定系数法即可求解.
解答 解:∵点A(a,b)在双曲线y=$\frac{5}{x}$上,
∴ab=5,
∵a、b都是正整数,
∴a=1,b=5或a=5,b=1.
设经过B(a,0)、C(0,b)两点的一次函数的解析式为y=mx+n.
①当a=1,b=5时,
由题意,得$\left\{\begin{array}{l}{m+n=0}\\{n=5}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-5}\\{n=5}\end{array}\right.$,
∴y=-5x+5;
②当a=5,b=1时,
由题意,得$\left\{\begin{array}{l}{5m+n=0}\\{n=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-\frac{1}{5}}\\{n=1}\end{array}\right.$,
∴y=-$\frac{1}{5}$x+1.
则所求解析式为y=-5x+5或y=-$\frac{1}{5}$x+1.
故答案为y=-5x+5或y=-$\frac{1}{5}$x+1.
点评 本题考查了反比例函数图象上点的坐标特征,待定系数法求一次函数的解析式.正确求出a、b的值是解题的关键.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
18.一个不透明的袋中装有5个红球、4个白球和3个黄球,每个球除颜色外完全相同,从中任意摸出一个球,下列说法不正确的是( )
| A. | 摸到红球、白球、黄球的概率相同 | B. | 摸到白球的概率是$\frac{1}{3}$ | ||
| C. | 摸到黄球的概率为$\frac{1}{4}$ | D. | 摸到红球的概率为$\frac{5}{12}$ |
15. 如图,下列条件中不能判定AB∥CD的是( )
如图,下列条件中不能判定AB∥CD的是( )
 如图,下列条件中不能判定AB∥CD的是( )
如图,下列条件中不能判定AB∥CD的是( )| A. | ∠3=∠4 | B. | ∠1=∠5 | C. | ∠1+∠4=180° | D. | ∠3=∠5 |
2.若a2-ab=0(b≠0),则$\frac{a}{a+b}$=( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 0或$\frac{1}{2}$ | D. | 1或 2 |
12.下列说法正确的是( )
| A. | 要了解某公司生产的100万只灯泡的使用寿命,可以采用抽样调查的方法 | |
| B. | 4位同学的数学期末成绩分别为100、95、105、110,则这四位同学数学期末成绩的中位数为100 | |
| C. | 甲乙两人各自跳远10次,若他们跳远成绩的平均数相同,甲乙跳远成绩的方差分别为0.51和0.62 | |
| D. | 某次抽奖活动中,中奖的概率为$\frac{1}{50}$表示每抽奖50次就有一次中奖 |
4.某商场销售国内品牌“华为”、国外品牌“苹果”两种智能手机,这两种手机其中一款的进价和售价如表所示:
该商场原计划购进该款华为、苹果手机各30部、20部,通过市场调研,商场决定减少苹果手机的购进数量,增加华为手机的购进数量,已知华为手机增加的数量是苹果手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元.
(1)苹果手机至少购进多少部?
(2)该商场应该怎样进货,使全国销售后获得的毛利润最大?并求出最大毛利润.
| 华为手机 | 苹果手机 | |
| 进价(元/部) | 2000 | 4400 |
| 售价(元/部) | 2500 | 5000 |
(1)苹果手机至少购进多少部?
(2)该商场应该怎样进货,使全国销售后获得的毛利润最大?并求出最大毛利润.
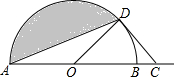 如图,AB为半圆O的直径,AB=4,C为AB延长线上一点,BC=2$\sqrt{2}$-2,过点作半圆的切线,切点为D,连接AD,则阴影部分的面积为$\frac{3}{2}$π-$\sqrt{2}$.
如图,AB为半圆O的直径,AB=4,C为AB延长线上一点,BC=2$\sqrt{2}$-2,过点作半圆的切线,切点为D,连接AD,则阴影部分的面积为$\frac{3}{2}$π-$\sqrt{2}$.


