题目内容
6. 如图,在△ABC中,∠ACB=90°,AC=2.8,BC=2.1,则高CD=1.68.
如图,在△ABC中,∠ACB=90°,AC=2.8,BC=2.1,则高CD=1.68.
分析 先根据勾股定理求出AB的长,再由三角形的面积公式即可得出结论.
解答 解:∵在△ABC中,∠ACB=90°,AC=2.8,BC=2.1,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{(2.8)^{2}+(2.1)^{2}}$=3.5.
∵AB•CD=AC•BC,
∴CD=$\frac{AC•BC}{AB}$=$\frac{2.8×2.1}{3.5}$=1.68.
故答案为:1.68.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
16.下列运算正确的是( )
| A. | x3+x5=x8 | B. | x3+x5=x15 | C. | (x+1)(x-1)=x2-1 | D. | (2x)5=2x5 |
14.下列分式变形正确的是( )
| A. | -$\frac{2x-3}{x}$=$\frac{-2x-3}{x}$ | B. | $\frac{2x-3}{x}$=$\frac{x-1.5}{x}$ | C. | $\frac{2x-3}{x}$=$\frac{2x}{x+3}$ | D. | $\frac{2x-3}{x}$=2-$\frac{3}{x}$ |
1.下列图形中的曲线不表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
18.一个不透明的袋中装有5个红球、4个白球和3个黄球,每个球除颜色外完全相同,从中任意摸出一个球,下列说法不正确的是( )
| A. | 摸到红球、白球、黄球的概率相同 | B. | 摸到白球的概率是$\frac{1}{3}$ | ||
| C. | 摸到黄球的概率为$\frac{1}{4}$ | D. | 摸到红球的概率为$\frac{5}{12}$ |
15. 如图,下列条件中不能判定AB∥CD的是( )
如图,下列条件中不能判定AB∥CD的是( )
 如图,下列条件中不能判定AB∥CD的是( )
如图,下列条件中不能判定AB∥CD的是( )| A. | ∠3=∠4 | B. | ∠1=∠5 | C. | ∠1+∠4=180° | D. | ∠3=∠5 |
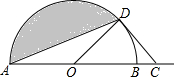 如图,AB为半圆O的直径,AB=4,C为AB延长线上一点,BC=2$\sqrt{2}$-2,过点作半圆的切线,切点为D,连接AD,则阴影部分的面积为$\frac{3}{2}$π-$\sqrt{2}$.
如图,AB为半圆O的直径,AB=4,C为AB延长线上一点,BC=2$\sqrt{2}$-2,过点作半圆的切线,切点为D,连接AD,则阴影部分的面积为$\frac{3}{2}$π-$\sqrt{2}$. 如图,在6×10正方形网格中,每个小正方形的边长为1个单位长度,作△ABC关于点O的中心对称图形△A′B′C′.
如图,在6×10正方形网格中,每个小正方形的边长为1个单位长度,作△ABC关于点O的中心对称图形△A′B′C′.