题目内容
4.某商店销售面向中考生的计数跳绳,每根成本为20元,销售的前40天内的日销售量m(根)与时间t(天)的关系如表.| 时间t(天) | 1 | 3 | 8 | 10 | 26 | … |
| 日销售量m(件) | 51 | 49 | 44 | 42 | 26 | … |
(1)认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m(件)与t(天)之间的关系式;
(2)倾计算40天中哪一天的日销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中,该公司决定每销售一件商品就捐赠a元利润(a<3)给希望工程.公司通过销售记录发现,前20天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
分析 (1)从表格可看出每天比前一天少销售1件,所以判断为一次函数关系式,待定系数法求解可得解析式;
(2)日利润=日销售量×每件利润,据此分别表示前20天和后20天的日利润,根据函数性质求最大值后比较得出结论;
(3)列式表示前20天中每天扣除捐赠后的日销售利润,根据函数性质求a的取值范围.
解答 解:(1)由表格中数据可知,当时间t每增加1天,日销售量相应减少1件,
∴m与t满足一次函数关系,
设m=kt+b,将(1,51)、(3,49)代入,
得:$\left\{\begin{array}{l}{k+b=51}\\{3k+b=49}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=52}\end{array}\right.$,
∴m与t的函数关系为:m=-t+52;
(2)设日销售利润为P,
当1≤t≤20时,
P=(-t+52)($\frac{1}{4}$t+25-20)=-$\frac{1}{4}$(t-16)2+324,
∴当t=16时,P有最大值,最大值为324元;
当21≤t≤40时,
P=(-t+52)(-$\frac{1}{2}$t+40-20)=$\frac{1}{2}$(t-46)2-18,
∵当t<46时,P随t的增大而减小,
∴当t=21时,P取得最大值,最大值为$\frac{1}{2}$(21-46)2-18=294.4元;
∵324>294.5,
∴第16天时,销售利润最大,最大利润为324元;
(3)设前20天扣除捐赠后的日利润为W,
则W=(-t+52)($\frac{1}{4}$t+25-20-a)=-$\frac{1}{4}$[t-2(8+a)]2+a2-36a+324,
∴对称轴为t=16+2a,
∵1≤t≤20,
∴16+2a≥20,解得:a≥2,
即a≥2时,W随t的增大而增大,
又∵a<3,
∴2≤a<3.
点评 本题考查了二次函数的应用,解题的关键是:(1)熟练掌握各函数的性质和图象特征,针对所给条件作出初步判断后需验证其正确性;(2)最值问题需由函数的性质求解时,正确表达关系式是关键.同时注意自变量的取值范围.

 快捷英语周周练系列答案
快捷英语周周练系列答案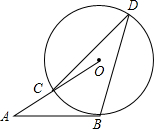 如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,D是优弧BC上一点,∠A=30°,则∠D为( )
如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,D是优弧BC上一点,∠A=30°,则∠D为( )| A. | 25° | B. | 30° | C. | 35° | D. | 45° |
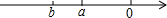 两个实数在数轴上对应点的位置如图所示,则a>b.(填“>”、“<”或“=”)
两个实数在数轴上对应点的位置如图所示,则a>b.(填“>”、“<”或“=”) 大客车和小轿车同时从甲地出发,沿笔直的公路以各自的速度匀速驶往异地,轿车到达乙地后,立即以相同的速度沿原路返回甲地,已知甲、乙两地相距180千米,大客车的速度为60千米/小时,轿车的速度为90千米/小时.设大客车和轿车出发x小时后,两车离乙地的距离分别为y1和y2千米.
大客车和小轿车同时从甲地出发,沿笔直的公路以各自的速度匀速驶往异地,轿车到达乙地后,立即以相同的速度沿原路返回甲地,已知甲、乙两地相距180千米,大客车的速度为60千米/小时,轿车的速度为90千米/小时.设大客车和轿车出发x小时后,两车离乙地的距离分别为y1和y2千米.