题目内容
16.下列各数$\frac{22}{7}$,-0.333…,3.14,$\frac{π}{2}$,0.1010010001…中,无理数的个数有( )个.| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
解答 解:$\frac{π}{2}$,0.1010010001…是无理数,
故选:B.
点评 此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
20.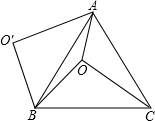 如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:
如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:
①△BO′A可以由△BOC绕点B逆时针旋转60°得到;
②点O与O′的距离为4;
③四边形AO BO′的面积为6+3$\sqrt{3}$
④∠AOB=150°;
⑤S△AOC+S△AOB=6+$\frac{9\sqrt{3}}{4}$.
其中正确的结论是( )
 如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:
如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;
②点O与O′的距离为4;
③四边形AO BO′的面积为6+3$\sqrt{3}$
④∠AOB=150°;
⑤S△AOC+S△AOB=6+$\frac{9\sqrt{3}}{4}$.
其中正确的结论是( )
| A. | ②③④⑤ | B. | ①③④⑤ | C. | ①②③⑤ | D. | ①②④⑤ |
1.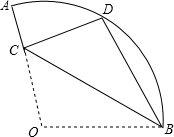 如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的度数为( )
如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的度数为( )
 如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的度数为( )
如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
8.如图四个图形中,是轴对称图形的有( )个


| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
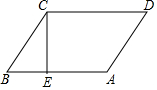 如图,平行四边形ABCD,AB=CD=9,AD=BC=5,(AB∥CD,AD∥BC),CE⊥AB于E,并且BE=3,CE=4.
如图,平行四边形ABCD,AB=CD=9,AD=BC=5,(AB∥CD,AD∥BC),CE⊥AB于E,并且BE=3,CE=4.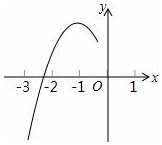 已知抛物线y=ax2+bx+c的顶点为D(-1,3),与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
已知抛物线y=ax2+bx+c的顶点为D(-1,3),与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图,则以下结论: