题目内容
14．在△ABC与△A′B′C′中，有：①$\frac{AB}{A′B′}$=$\frac{BC}{B′C′}$； ②$\frac{BC}{B′C′}$=$\frac{AC}{A′C′}$；③∠A=∠A′；④∠C=∠C′，如果从中任取两个组成一组，那么能判断△ABC∽△A′B′C′的共有组数是（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 根据相似三角形的判定定理：三条对应边的比相等的三角形相似可得需①②组合，对应边成比例且夹角相等的三角形相似可得②④组合，有两角对应相等的三角形相似可得③④组合，则可求得答案．
解答 解：①②组合，
∵$\frac{AB}{A′B′}$=$\frac{BC}{B′C′}$，$\frac{BC}{B′C′}$=$\frac{AC}{A′C′}$，
∴$\frac{AB}{A′B′}$=$\frac{BC}{B′C′}$=$\frac{AC}{A′C′}$；
∴△ABC∽△A′B′C′（三条对应边的比相等的三角形相似）；
②④组合，
∵$\frac{BC}{B′C′}$=$\frac{AC}{A′C′}$，∠C=∠C′，
∴△ABC∽△A′B′C′（对应边成比例且夹角相等的三角形相似）；
③④组合，
∵∠A=∠A′，∠C=∠C′，
∴△ABC∽△A′B′C′（有两角对应相等的三角形相似）．
∴能判断△ABC∽△A′B′C′的共有3组．
故选C．
点评 此题考查了相似三角形的判定．此题难度不大，解题的关键是熟记相似三角形的判定定理，掌握定理的应用．
练习册系列答案
相关题目
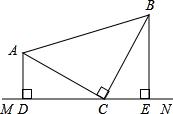如图，在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN，BE⊥MN，垂足分别为点D，E．求证：
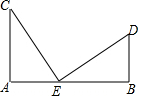如图，AC⊥AB，BD⊥AB，CE⊥DE，CE=DE．求证：AC+BD=AB．
9．下面条件中，不能证出Rt△ABC≌Rt△A'B'C'的是（ ）
| A． | AC=A'C'，BC=B'C' | B． | AB=A'B'，AC=A'C' | C． | AB=B'C'，AC=A'C' | D． | ∠B=∠B'，AB=A'B' |
