题目内容
2.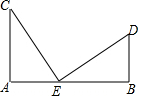 如图,AC⊥AB,BD⊥AB,CE⊥DE,CE=DE.求证:AC+BD=AB.
如图,AC⊥AB,BD⊥AB,CE⊥DE,CE=DE.求证:AC+BD=AB.
分析 根据垂直的定义得到∠A=∠B=90°,再证明∠C=∠DEB,即可证明△CAE≌△EBD,根据全等三角形的性质即可证得结论.
解答 证明:
∵AC⊥AB,BD⊥AB,
∴∠A=∠B=90°,
∴∠C+∠CEA=90°,∠D+∠DEB=90°,
∵CE⊥DE,
∴∠CED=90°,
∴∠CEA+∠DEB=90°,
∴∠C=∠DEB,
在△CAE和△EBD中
$\left\{\begin{array}{l}{∠A=∠B=90°}\\{∠C=∠DEB}\\{CE=DE}\end{array}\right.$,
∴△CAE≌△EBD(AAS),
∴AC=BE,BD=AE,
∵AE+BE=AB,
∴AC+BD=AB
点评 本题主要考查了互为余角的关系,全等三角形的判定与性质,能根据同角的余角相等证得∠C=∠DEB是解决问题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
10.若正实数a、b满足ab=a+b+3,则a2+b2的最小值为( )
| A. | -7 | B. | 2 | C. | 9 | D. | 18 |
12.用一根铁丝围成一个长为24cm、宽为12cm的长方形,如果将它改制成一个正方形,这个正方形的面积是( )
| A. | 81cm2 | B. | 18cm2 | C. | 324cm2 | D. | 326cm2 |
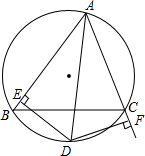 如图,△ABC中,∠A的角平分线交△ABC的外接圆于点D,DE⊥AB于E,DF⊥AC交AC的延长线于F,求证:BE=CF.
如图,△ABC中,∠A的角平分线交△ABC的外接圆于点D,DE⊥AB于E,DF⊥AC交AC的延长线于F,求证:BE=CF.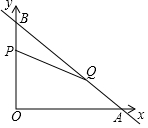 如图,平面直角坐标系xOy 中,直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于点A、B,动点P从点B出发在线段BO上以每秒1个单位长度的速度向终点O移动,同时动点Q从点A出发在线段AB上以每秒2个单位长度的速度向终点B移动,当其中一个点运动到终点时,另一个点也随之停止运动,设点P,Q移动的时间为t秒.
如图,平面直角坐标系xOy 中,直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于点A、B,动点P从点B出发在线段BO上以每秒1个单位长度的速度向终点O移动,同时动点Q从点A出发在线段AB上以每秒2个单位长度的速度向终点B移动,当其中一个点运动到终点时,另一个点也随之停止运动,设点P,Q移动的时间为t秒.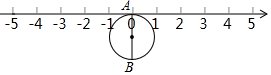 如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(注:结果保留π )
如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(注:结果保留π ) 如图,已知△ABC,用直尺和圆规作△ABC的角平分线BD、高CE.(不必写画法,保留作图痕迹)
如图,已知△ABC,用直尺和圆规作△ABC的角平分线BD、高CE.(不必写画法,保留作图痕迹)