题目内容
14．已知$\sqrt{2x-3}+\sqrt{y+2}$=$\sqrt{z-2}+\sqrt{2-z}$在实数范围成立，那么xyz的值是多少？分析 先根据二次根式有意义的条件求出z的值，再由非负数的性质求出x、y的值，进而可得出结论．
解答 解：∵$\sqrt{z-2}$与$\sqrt{2-z}$有意义，
∴$\left\{\begin{array}{l}z-2≥0\\ 2-z≥0\end{array}\right.$，解得z=2，
∴$\sqrt{2x-3}$+$\sqrt{y+2}$=0，
∴2x-3=0，y+2=0，
解得x=$\frac{3}{2}$，y=-2，
∴xyz=$\frac{3}{2}$×（-2）×2=-6．
点评 本题考查的是非负数的性质，熟知算术平方根具有非负性是解答此题的关键．
练习册系列答案
相关题目
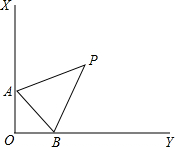如图所示，∠XOY=90°，点A，B分别为射线OX，OY上两点，∠XAB和∠YBA的角平分线交于点P，则当A，B移动时，∠P的大小是否发生变化？如果保持不变，请说明理由；如果随A，B的移动而变化，请求出变化范围．
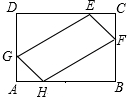如图，在矩形ABCD中，AB=8，BC=4，点H、F、E、G分别在AB、BC、CD、DA上，且AH=AG=CE=CF=x，四边形EFHG的面积为y．