题目内容
6.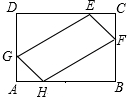 如图,在矩形ABCD中,AB=8,BC=4,点H、F、E、G分别在AB、BC、CD、DA上,且AH=AG=CE=CF=x,四边形EFHG的面积为y.
如图,在矩形ABCD中,AB=8,BC=4,点H、F、E、G分别在AB、BC、CD、DA上,且AH=AG=CE=CF=x,四边形EFHG的面积为y.(1)求y与x之间的函数关系式;
(2)当x为何值时.四边形EFHG的面积最大?
分析 (1)由矩形的性质得出∠A=∠B=∠C=∠D=90°,CD=AB=8,AD=BC=4,得出BH=DE=8-x,DG=BF=4-x,四边形EFHG的面积=矩形ABCD的面积-△AGH的面积-△CEF的面积-△BFH的面积-△DEG的面积,即可得出结果;
(2)先把二次函数化成配方后的形式,由二次函数的性质即可得出结果.
解答 解:(1)∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90°,CD=AB=8,AD=BC=4,
∵AH=AG=CE=CF=x,
∴BH=DE=8-x,DG=BF=4-x,
∴四边形EFHG的面积=矩形ABCD的面积-△AGH的面积-△CEF的面积-△BFH的面积-△DEG的面积
=8×4-$\frac{1}{2}$x2-$\frac{1}{2}$x2-$\frac{1}{2}$(8-x)(4-x)-$\frac{1}{2}$(8-x)(4-x)=-2x2+12x,
即y与x之间的函数关系式为:y=-2x2+12x;
(2)∵y=-2x2+12x=-2(x-3)2+18,-2<0,
∴y有最大值,
当x=3时,y的最大值=18,
即当x=3时,四边形EFHG的面积最大=18.
点评 本题考查了矩形的性质、三角形和四边形面积的计算、二次函数的最值;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,AD是BC边上的中线,E、F是AC边的三等分点,连接BE交AD于G,连接DF,求AG:AD的值.
如图,在△ABC中,AD是BC边上的中线,E、F是AC边的三等分点,连接BE交AD于G,连接DF,求AG:AD的值.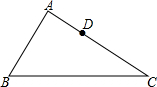 如图,△ABC中,AB=12,AC=15,D为AC上一点,CD=$\frac{2}{3}$AC,在AB边上找一点E,使得△ADE与△ABC相似,求AE的长.
如图,△ABC中,AB=12,AC=15,D为AC上一点,CD=$\frac{2}{3}$AC,在AB边上找一点E,使得△ADE与△ABC相似,求AE的长.