题目内容
9.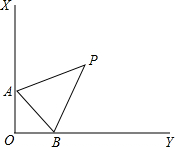 如图所示,∠XOY=90°,点A,B分别为射线OX,OY上两点,∠XAB和∠YBA的角平分线交于点P,则当A,B移动时,∠P的大小是否发生变化?如果保持不变,请说明理由;如果随A,B的移动而变化,请求出变化范围.
如图所示,∠XOY=90°,点A,B分别为射线OX,OY上两点,∠XAB和∠YBA的角平分线交于点P,则当A,B移动时,∠P的大小是否发生变化?如果保持不变,请说明理由;如果随A,B的移动而变化,请求出变化范围.
分析 根据三角形内角和定理得到∠A+∠B=90°,根据平角的定义得到∠XAB+∠YBA=270°,根据角平分线的定义得到∠PAB+∠PBA=135°,根据三角形内角和定理计算得到答案.
解答 解:∠P的大小不变.
∵∠A+∠B=90°,
∴∠XAB+∠YBA=270°,
∵AP、BP分别是∠XAB和∠YBA的平分线,
∴∠PAB=$\frac{1}{2}$∠XAB,∠PBA=$\frac{1}{2}$∠YBA,
∴∠PAB+∠PBA=135°,
则∠P=180°-(∠PAB+∠PBA)=45°.
点评 本题考查的是三角形内角和定理和角平分线的定义,掌握三角形内角和等于180°是解题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
19.若等腰△ABC的两边长分别是4和7,则其周长为( )
| A. | 14 | B. | 15 | C. | 18 | D. | 15或18 |
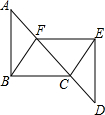 如图,已知A,F,C,D四点在同一条直线上,AF=CD,∠A=∠D,AB=DE,则BC=EF,请说明理由(完成下列填空)
如图,已知A,F,C,D四点在同一条直线上,AF=CD,∠A=∠D,AB=DE,则BC=EF,请说明理由(完成下列填空)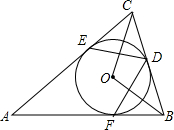 如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠A=40°,求∠BOC和∠EDF的度数.
如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠A=40°,求∠BOC和∠EDF的度数.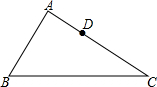 如图,△ABC中,AB=12,AC=15,D为AC上一点,CD=$\frac{2}{3}$AC,在AB边上找一点E,使得△ADE与△ABC相似,求AE的长.
如图,△ABC中,AB=12,AC=15,D为AC上一点,CD=$\frac{2}{3}$AC,在AB边上找一点E,使得△ADE与△ABC相似,求AE的长.