题目内容
19.下列四组线段中,可以构成直角三角形的是( )| A. | 2,3,4 | B. | 4,5,6 | C. | 1,$\sqrt{2}$,$\sqrt{3}$ | D. | 1,$\sqrt{2}$,3 |
分析 根据勾股定理的逆定理求出两小边的平方和和大边的平方,看看是否相等即可.
解答 解:A、32+22≠42,即三角形不是直角三角形,故本选项错误;
B、42+52≠62,即三角形不是直角三角形,故本选项错误;
C、12+($\sqrt{2}$)2=($\sqrt{3}$)2,即三角形是直角三角形,故本选项正确;
D、12+($\sqrt{2}$)2≠32,即三角形不是直角三角形,故本选项错误;
故选C.
点评 本题考查了勾股定理的逆定理的应用,注意:如果一个三角形的两边的平方和等于第三边的平方,那么这个三角形是直角三角形,难度适中.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
9. 实数a、b在数轴上的位置如图所示,则下列各式表示正确的是( )
实数a、b在数轴上的位置如图所示,则下列各式表示正确的是( )
 实数a、b在数轴上的位置如图所示,则下列各式表示正确的是( )
实数a、b在数轴上的位置如图所示,则下列各式表示正确的是( )| A. | b-a<0 | B. | 1-a>0 | C. | b-1>0 | D. | -1-b<0 |
10.$\sqrt{26}$-2的值在( )
| A. | 2、3之间 | B. | 3、4之间 | C. | 5、6之间 | D. | 6、7之间 |
7.观察下列等式:
①32-4×12=5;②52-4×22=9;③72-4×32=13;…
根据上述式子的规律,解答下列问题:
(1)第④个等式为92-4×42=17;
(2)写出第n个等式,并说明其正确性.
①32-4×12=5;②52-4×22=9;③72-4×32=13;…
根据上述式子的规律,解答下列问题:
(1)第④个等式为92-4×42=17;
(2)写出第n个等式,并说明其正确性.
8.下列计算正确的是( )
| A. | $\sqrt{3}$+$\sqrt{7}$=$\sqrt{10}$ | B. | 7$\sqrt{7}$-2$\sqrt{2}$=5$\sqrt{5}$ | C. | 2$\sqrt{2}$×3$\sqrt{2}$=6$\sqrt{2}$ | D. | $\sqrt{2}$÷$\sqrt{5}$=$\frac{\sqrt{10}}{5}$ |
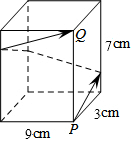 如图,长方体的底面边长分别为9cm和3cm,高为7cm,若一只蚂蚁从P开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为25cm.
如图,长方体的底面边长分别为9cm和3cm,高为7cm,若一只蚂蚁从P开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为25cm.