题目内容
7．
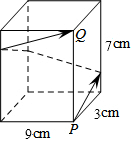如图，长方体的底面边长分别为9cm和3cm，高为7cm，若一只蚂蚁从P开始经过4个侧面爬行一圈到达Q点，则蚂蚁爬行的最短路径长为25cm．
分析 要求长方体中两点之间的最短路径，最直接的作法，就是将长方体展开，然后利用两点之间线段最短解答．
解答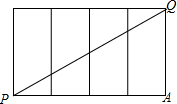 
解：如图所示：
∵长方体的底面边长分别为9cm和3cm，高为7cm，．
∴PA=9+9+3+3=24（cm），QA=7cm，
∴PQ=$\sqrt{P{A}^{2}+A{Q}^{2}}$=$\sqrt{2{4}^{2}+{7}^{2}}$=25（cm）．
故答案是：25．
点评 本题的是平面展开-最短路径问题，解答此类问题时要先根据题意把立体图形展开成平面图形后，再确定两点之间的最短路径．一般情况是两点之间，线段最短．在平面图形上构造直角三角形解决问题．
练习册系列答案
考前必练系列答案
相关题目
17．下列计算中，正确的是（ ）
| A． | $\sqrt{18}$÷$\sqrt{2}$=$\sqrt{6}$ | B． | （4$\sqrt{2}$）2=8 | C． | $\sqrt{（-2）^{2}}$=2 | D． | 2$\sqrt{3}$×2$\sqrt{2}$=2$\sqrt{6}$ |
如图，已知直线a∥b，点A在直线a上，点B、C在直线b上，点P在线段AB上，∠1=70°，∠2=100°，那么∠PCB=30度．
15．某产品每件成本150元，销售阶段每件产品的销售价x（元）与产品的月销售量y（件）之间的关系如下表：若月销售量是销售价的一次函数．
求：（1）求出月销售量y（件）与销售价x（元）的函数关系式；
（2）求销售价定为240元时，每月的销售利润．
| x（元） | 180 | 200 | 220 | … |
| y （件） | 850 | 750 | 650 | … |
（2）求销售价定为240元时，每月的销售利润．
12．下列说法中正确的是（ ）
| A． | 两条射线所组成的图形叫角 | |
| B． | 角的大小与所画的角的边的长短无关 | |
| C． | 角的两边是两条线段 | |
| D． | 角的两边是两条直线 |
19．下列四组线段中，可以构成直角三角形的是（ ）
| A． | 2，3，4 | B． | 4，5，6 | C． | 1，$\sqrt{2}$，$\sqrt{3}$ | D． | 1，$\sqrt{2}$，3 |