题目内容
13.若关于x的方程x2+(2a-1)x+a2-1=0的两根是x1、x2,且(3x1-x2)(x1-3x2)+21=0,则a的值为-5.分析 首先根据方程有两个根求出a的取值范围,然后根据根与系数的关系把(3x1-x2)(x1-3x2)+21=0转化为a2+3a-10=0,最后解一元二次方程求出a的值.
解答 解:∵x2+(2a-1)x+a2-1=0的两根是x1、x2,
∴△=(2a-1)2-4(a2-1)=-4a+5≥0,
∴a≤$\frac{5}{4}$,
∴x1+x2=1-2a,x1x2=a2-1,
∵(3x1-x2)(x1-3x2)+21=0,
∴3x12-10x1x2+3x22+21=0,
∴3(x1+x2)2-16x1x2+21=0,
∴3(1-2a)2-16(a2-1)+21=0,
∴a2+3a-10=0,
∴a1=-5,a2=2,
∵a≤$\frac{5}{4}$,
∴a=-5,
故答案为-5.
点评 本题主要考查了根与系数的关系的知识,解答本题的关键是能根据根与系数的关系把(3x1-x2)(x1-3x2)+21=0转化为a的一元二次方程,此题难度不大.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
1. 如图,⊙O内切于△ABC,切点D,E,F分别在BC,AB,AC上.已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( )
如图,⊙O内切于△ABC,切点D,E,F分别在BC,AB,AC上.已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( )
 如图,⊙O内切于△ABC,切点D,E,F分别在BC,AB,AC上.已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( )
如图,⊙O内切于△ABC,切点D,E,F分别在BC,AB,AC上.已知∠B=50°,∠C=60°,连结OE,OF,DE,DF,那么∠EDF等于( )| A. | 40° | B. | 55° | C. | 65° | D. | 70° |
8.若圆锥的母线长是底面半径的3倍,则将圆锥的侧面展开后的扇形的圆心角是( )
| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
18.下列运算正确的是( )
| A. | a3+a=2a4 | B. | a6÷a-3=a3 | C. | a3•a3=2a3 | D. | (-2a2)3=-8a6 |
2.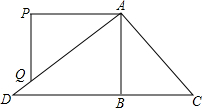 如图,将△ABC绕点A按顺时针方向旋转某个角度得到△APQ,使AP平行于CB,CB,AQ的延长线相交于点D.如果∠D=40°,则∠BAC的度数为( )
如图,将△ABC绕点A按顺时针方向旋转某个角度得到△APQ,使AP平行于CB,CB,AQ的延长线相交于点D.如果∠D=40°,则∠BAC的度数为( )
 如图,将△ABC绕点A按顺时针方向旋转某个角度得到△APQ,使AP平行于CB,CB,AQ的延长线相交于点D.如果∠D=40°,则∠BAC的度数为( )
如图,将△ABC绕点A按顺时针方向旋转某个角度得到△APQ,使AP平行于CB,CB,AQ的延长线相交于点D.如果∠D=40°,则∠BAC的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
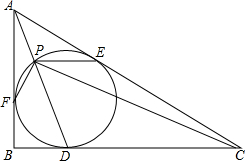 在直角三角形ABC中,∠B=90°,它的内切圆分别与边BC,CA,AB相切与点D,E,F,连接AD,与内切圆相交于另一点P,连接PC,PE,PF.已知PC⊥PF,求证:
在直角三角形ABC中,∠B=90°,它的内切圆分别与边BC,CA,AB相切与点D,E,F,连接AD,与内切圆相交于另一点P,连接PC,PE,PF.已知PC⊥PF,求证: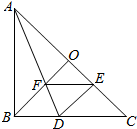 如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连结DE、EF.下列结论:①tan∠ADB=2;②图中有4对全等三角形;③BD=BF;④S四边形DFOE=S△AOF;⑤若将△DEF沿EF折叠,则点D一定落在AC上,上述结论中正确的个数是( )
如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连结DE、EF.下列结论:①tan∠ADB=2;②图中有4对全等三角形;③BD=BF;④S四边形DFOE=S△AOF;⑤若将△DEF沿EF折叠,则点D一定落在AC上,上述结论中正确的个数是( )