题目内容
3.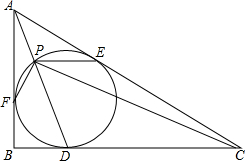 在直角三角形ABC中,∠B=90°,它的内切圆分别与边BC,CA,AB相切与点D,E,F,连接AD,与内切圆相交于另一点P,连接PC,PE,PF.已知PC⊥PF,求证:
在直角三角形ABC中,∠B=90°,它的内切圆分别与边BC,CA,AB相切与点D,E,F,连接AD,与内切圆相交于另一点P,连接PC,PE,PF.已知PC⊥PF,求证:(1)PD平分∠FPC;
(2)PE∥BC.
分析 (1)证明三角形相似只要知道两个角相等即可,根据弦切角定理很容易的出∠PFD=∠PDC,由角度关系可以知道∠FPD=DPC,即可证明.
(2)根据AE、AF与圆相切,由弦切角定理推出△AFP∽△ADF,△AEP∽△ADE,得到对应边成比例,通过等量代换得到比例式又证得三角形相似,得到△EPD也是等腰三角形,于是得到结论.
解答 解:(1)∵BC与圆相切,
∴∠PFD=∠PDC.
∵BF、BD分别于圆相切,
∴∠BFD=∠BDF=45°.
∴∠FPD=45°.
∵PC⊥PF,
∴∠FPD=∠DPC.
故PD平分∠FPC;
(2))∵AE、AF与圆相切,
∴∠AFP=∠ADF,∠AEP=∠ADE,
∵∠FAD=∠PAF,∠EAP=∠DAE,
∴△AFP∽△ADF,△AEP∽△ADE,
∴$\frac{PF}{FD}=\frac{PD}{DC}$,
∴$\frac{EP}{DE}=\frac{AP}{AE}=\frac{AP}{AF}=\frac{FP}{DF}$,
∴$\frac{EP}{DE}=\frac{PD}{DC}$.
∵∠EPD=∠EDC,
∴△EPD∽△EDC,
∴△EPD也是等腰三角形,
∴∠PED=∠EPD=∠EDC,
∴PE∥BC.
点评 本题主要考查三角形相切的性质,结合角度关系来求.注意线段之间的转化,特别是证明三角形相似是个难点.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
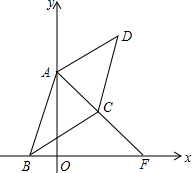 如图,若A(0,a),B(b,0),C(c,c),且(a-5)2+|b+2|+$\sqrt{c-3}$=0.四边形ABCD为平行四边形,点D在第一象限,直线AC交x轴于点F.
如图,若A(0,a),B(b,0),C(c,c),且(a-5)2+|b+2|+$\sqrt{c-3}$=0.四边形ABCD为平行四边形,点D在第一象限,直线AC交x轴于点F.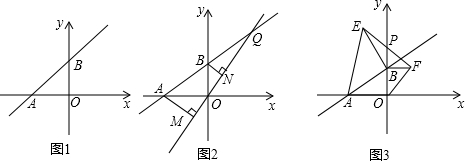
 如图,⊙O与△ABC各边切于点D、E、F,且∠C=60°,∠EOF=100°,求∠B的度数.
如图,⊙O与△ABC各边切于点D、E、F,且∠C=60°,∠EOF=100°,求∠B的度数.