题目内容
19.有一所寄宿制学校,开学安排宿舍时,如果每间宿舍安排住4人,将会空出5间宿舍;如果每间宿舍安排住3人,就有100人没床位,那么在学校住宿的学生有多少人?设在学校住宿的学生有x人,则可列方程( )| A. | $\frac{x}{4}+5=\frac{x-100}{3}$ | B. | $\frac{x}{4}+5=\frac{x}{3}-100$ | C. | $\frac{x+5}{4}=\frac{x-100}{3}$ | D. | $\frac{x}{4}-5=\frac{x+100}{3}$ |
分析 设在学校住宿的学生有x人,根据学校宿舍间数一定,列出一元一次方程即可.
解答 解:设在学校住宿的学生有x人,
每间宿舍安排住4人,需要宿舍$\frac{x}{4}$间,
每间宿舍安排住3人,100人没有床位,
则x-100人住上宿舍,宿舍房间为$\frac{x-100}{3}$间,
即$\frac{x}{4}$+5=$\frac{x-100}{3}$,
故选A.
点评 本题主要考查了由实际问题抽象出一元一次方程的知识,解题的关键是根据宿舍间数一定列方程,此题难度不大.

练习册系列答案
相关题目
9.下列多项式在实数范围内可以因式分解的是( )
| A. | x2-x+6 | B. | x2+9x-6 | C. | x2+x+6 | D. | 2x2-x+1 |
7.下列事件中是不可能事件的是( )
| A. | 降雨时水位上升 | B. | 在南极点找到东西方向 | ||
| C. | 体育运动时消耗卡路里 | D. | 体育运动中肌肉拉伤 |
14.如果平行四边形ABCD对角线AC与BD交于O,$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{BC}$=$\overrightarrow b$,那么下列向量中与向量$\frac{1}{2}$($\overrightarrow a$+$\overrightarrow b$)相等的是( )
| A. | $\overrightarrow{AO}$ | B. | $\overrightarrow{DO}$ | C. | $\overrightarrow{CO}$ | D. | $\overrightarrow{BO}$ |
11.在Rt△ABC中,∠C=90°,∠A=50°,则∠B=( )
| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
8.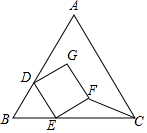 如图为等边△ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB、BC上,且BD=BE,若AB=3,DE=1,则△EFC的面积为( )
如图为等边△ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB、BC上,且BD=BE,若AB=3,DE=1,则△EFC的面积为( )
 如图为等边△ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB、BC上,且BD=BE,若AB=3,DE=1,则△EFC的面积为( )
如图为等边△ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB、BC上,且BD=BE,若AB=3,DE=1,则△EFC的面积为( )| A. | $\frac{1}{4}$ | B. | 1 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
 要对一块长为60米,宽为40米的长方形场地进行绿化和硬化,设计方案如图所示,长方形P、Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面的宽相等,并且两块绿地面积的和为长方形ABCD面积的$\frac{1}{4}$,求P、Q为两块绿地周围的硬化路面的宽.
要对一块长为60米,宽为40米的长方形场地进行绿化和硬化,设计方案如图所示,长方形P、Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面的宽相等,并且两块绿地面积的和为长方形ABCD面积的$\frac{1}{4}$,求P、Q为两块绿地周围的硬化路面的宽. 用20米长的篱笆围成一个一边靠墙的长方形仓库(如图所示),若要求围成的长方形面积为60米2,并且这堵墙长10米,在与墙平行的一边,开一扇宽2米的门(门不占用篱笆材料),问:该长方形相邻两边长要取多少米?
用20米长的篱笆围成一个一边靠墙的长方形仓库(如图所示),若要求围成的长方形面积为60米2,并且这堵墙长10米,在与墙平行的一边,开一扇宽2米的门(门不占用篱笆材料),问:该长方形相邻两边长要取多少米? y=ax2+bx+c(a≠0)的图象如图,则下列判断正确的有( )
y=ax2+bx+c(a≠0)的图象如图,则下列判断正确的有( )