题目内容
在△ABC和△A′B′C′中,
=
=
=
,且△ABC的周长为15cm,求△A′B′C′的周长.
| AB |
| A′B′ |
| BC |
| B′C′ |
| CA |
| C′A′ |
| 1 |
| 2 |
考点:相似三角形的判定与性质
专题:
分析:直接运用三边对应成比例来判断两三角形相似,进而利用性质来求解.
解答:解:∵
=
=
=
,
∴△ABC∽△A′B′C′;
设△ABC与△A′B′C′的周长分别为xcm,ycm;
∵△ABC∽△A′B′C,且相似比为
,
∴
=
,而x=15cm,
∴y=30cm,
即△A′B′C′的周长为30cm.
| AB |
| A′B′ |
| BC |
| B′C′ |
| CA |
| C′A′ |
| 1 |
| 2 |
∴△ABC∽△A′B′C′;
设△ABC与△A′B′C′的周长分别为xcm,ycm;
∵△ABC∽△A′B′C,且相似比为
| 1 |
| 2 |
∴
| x |
| y |
| 1 |
| 2 |
∴y=30cm,
即△A′B′C′的周长为30cm.
点评:该命题考查了相似三角形的判定及其性质的应用问题;解题的关键是灵活运用有关性质来分析、判断、证明或求解.

练习册系列答案
相关题目
有一列数a1,a2,a3,a4,…,an,从第二个数开始,每一个数都等于1与它前面那个数的差的倒数,若a1=3,则a2014为( )
| A、2014 | ||
B、
| ||
C、-
| ||
| D、3 |
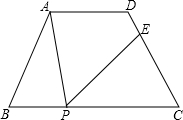 如图,在四边形ABCD中,AD∥BC,∠B=∠C=60°,AD=3,BC=7,P为BC边上的一点(不与B、C重合),过点P作∠APE=∠B,PE交CD于点E.若CE=3,求PE的长.
如图,在四边形ABCD中,AD∥BC,∠B=∠C=60°,AD=3,BC=7,P为BC边上的一点(不与B、C重合),过点P作∠APE=∠B,PE交CD于点E.若CE=3,求PE的长. 如图,在直角坐标系中,正方形ABCD的顶点B在x轴上,顶点C在y轴上,若AB=2,∠CBO=30°,试写出顶点A、B的坐标.
如图,在直角坐标系中,正方形ABCD的顶点B在x轴上,顶点C在y轴上,若AB=2,∠CBO=30°,试写出顶点A、B的坐标.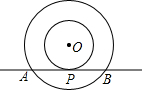 如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点.求证:AP=BP.
如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点.求证:AP=BP.