题目内容
在☉O中
=2
,则弦AB与弦CD的大小关系是( )
 |
| AB |
 |
| CD |
| A、AB>2CD |
| B、AB=2CD |
| C、AB<2CD |
| D、AB=CD |
考点:圆心角、弧、弦的关系,三角形三边关系
专题:
分析:根据两弧的关系,作出
的中点E,则AE=BE=CD,根据三角形两边之和大于第三边就可以得到结论.
 |
| AB |
解答: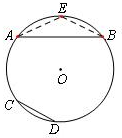 解:AB<2CD.
解:AB<2CD.
取
的中点E,连接EA、EB,则
=
=
,
所以EA=EB=CD,
在△ABE中,AE+BE>AB,即2CD>AB,
则AB<2CD,
∴CD<AB<2CD,
故选C.
 解:AB<2CD.
解:AB<2CD.取
 |
| AB |
 |
| EA |
 |
| EB |
 |
| CD |
所以EA=EB=CD,
在△ABE中,AE+BE>AB,即2CD>AB,
则AB<2CD,
∴CD<AB<2CD,
故选C.
点评:本题主要考查了:在同圆或等圆中圆心角相等,弧相等,弦相等,弦心距相等,在这几组相等关系中,只要有一组成立,则另外几组一定成立.

练习册系列答案
相关题目
有一列数a1,a2,a3,a4,…,an,从第二个数开始,每一个数都等于1与它前面那个数的差的倒数,若a1=3,则a2014为( )
| A、2014 | ||
B、
| ||
C、-
| ||
| D、3 |
 如图,AD平分∠BAC,AB=AC,那么判定△ABD≌△ACD的理由是( )
如图,AD平分∠BAC,AB=AC,那么判定△ABD≌△ACD的理由是( )| A、SSS | B、SAS |
| C、ASA | D、AAS |
点P(a,4)与点Q(2,b)关于x轴对称,则a、b的值是( )
| A、a=2,b=4 |
| B、a=2,b=-4 |
| C、a=-2,b=4 |
| D、a=-2,b=-4 |
下列说法正确的是( )
| A、9的算术平方根是3 |
| B、4的平方根是2 |
| C、8的立方根是±2 |
| D、-8没有立方根 |
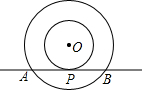 如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点.求证:AP=BP.
如图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点.求证:AP=BP.