题目内容
14.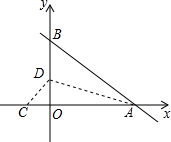 如图,在平面直角坐标系xOy中,直线y=-$\frac{4}{3}$x+3与x轴交于点A,与y轴交于点B,将△AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记作点C,折痕与y轴交于点D,则C、D两点的坐标分别为C (-$\frac{3}{2}$,0),D(0,$\frac{4}{3}$).
如图,在平面直角坐标系xOy中,直线y=-$\frac{4}{3}$x+3与x轴交于点A,与y轴交于点B,将△AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记作点C,折痕与y轴交于点D,则C、D两点的坐标分别为C (-$\frac{3}{2}$,0),D(0,$\frac{4}{3}$).
分析 由折叠的性质得到△ABD≌△ACD,由全等三角形的性质得出BD=CD,AB=AC,由一次函数解析式求出A与B坐标,确定出OA与OB的长,由勾股定理求出AB,得出AC、OC,得出点C的坐标;设CD=x,则OD=3-x,利用勾股定理得出方程求出x的值,即可得出点D坐标.
解答 解:由折叠的性质得:△ADB≌△ADC,
∴AB=AC,BD=CD,
对于直线y=-$\frac{4}{3}$x+3,
令x=0,得到y=3;令y=0,得到x=$\frac{9}{4}$,
∴A($\frac{9}{4}$,0),B(0,3),
∴OA=$\frac{9}{4}$,OB=3,
在Rt△AOB中,根据勾股定理得:
AB=$\sqrt{(\frac{9}{4})^{2}+{3}^{2}}$=$\frac{15}{4}$,
∴OC=AC-OA=AB-OA=$\frac{15}{4}$-$\frac{9}{4}$=$\frac{3}{2}$,
∴C(-$\frac{3}{2}$,0);
在Rt△COD中,设CD=BD=x,则OD=3-x,
根据勾股定理得:x2=(3-x)2+1,
解得:x=$\frac{5}{3}$,
∴OD=3-$\frac{5}{3}$=$\frac{4}{3}$,
∴D(0,$\frac{4}{3}$).
故答案为:(-$\frac{3}{2}$,0);(0,$\frac{4}{3}$ ).
点评 本题考查了翻折变换的性质、一次函数图象上点的坐标特征、全等三角形的性质、勾股定理;熟练掌握翻折变换的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
3.已知甲乙两组数据的平均数相等,若甲组数据的方差为0.022,乙组数据的方差为0.102,则( )
| A. | 甲组数据比乙组数据波动大 | B. | 乙组数据比甲组数据波动大 | ||
| C. | 甲组数据与乙组数据波动一样大 | D. | 甲乙两组数据波动不能比较 |
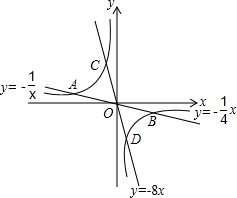 如图,已知双曲线y1=-$\frac{1}{x}$与两直线y2=-$\frac{1}{4}$x,y3=-8x,若无论x取何值,y总取y1,y2,y3中的最小值,则y的最大值为$\frac{1}{2}$.
如图,已知双曲线y1=-$\frac{1}{x}$与两直线y2=-$\frac{1}{4}$x,y3=-8x,若无论x取何值,y总取y1,y2,y3中的最小值,则y的最大值为$\frac{1}{2}$.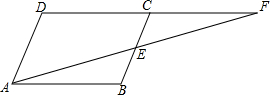 如图,在平行四边形ABCD中,E为BC的中点,AE的延长线与DC的延长线相交于F.
如图,在平行四边形ABCD中,E为BC的中点,AE的延长线与DC的延长线相交于F.
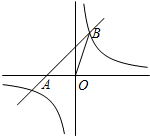 如图,一次函数y=x+2的图象交x轴于点A,且过点B(1,m).点B在反比例函数y=$\frac{k}{x}$(k≠0)的图象上.
如图,一次函数y=x+2的图象交x轴于点A,且过点B(1,m).点B在反比例函数y=$\frac{k}{x}$(k≠0)的图象上.