题目内容
2.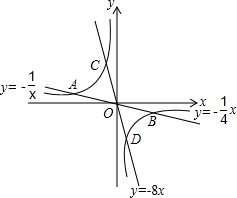 如图,已知双曲线y1=-$\frac{1}{x}$与两直线y2=-$\frac{1}{4}$x,y3=-8x,若无论x取何值,y总取y1,y2,y3中的最小值,则y的最大值为$\frac{1}{2}$.
如图,已知双曲线y1=-$\frac{1}{x}$与两直线y2=-$\frac{1}{4}$x,y3=-8x,若无论x取何值,y总取y1,y2,y3中的最小值,则y的最大值为$\frac{1}{2}$.
分析 y始终取三个函数的最小值,y最大值即求三个函数的公共部分的最大值.
解答 解:联立y1、y2可得$\left\{\begin{array}{l}{y=-\frac{1}{x}}\\{y=-\frac{1}{4}x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-2}\\{y=\frac{1}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=-\frac{1}{2}}\end{array}\right.$,
∴A(-2,$\frac{1}{2}$),B(2,-$\frac{1}{2}$),
∵无论x取何值,y总取y1,y2,y3中的最小值,
观察图象
∴y的最大值为A点的纵坐标,
∴y的最大值为$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题主要考查一次函数与反比例函数的交点问题,确定出y的最大值为三个函数公共部分的最大值是解题的关键.

练习册系列答案
相关题目
13.下列各式从左边到右边的变形中,是因式分解的是( )
| A. | (x+1)(x-1)=x2-1 | B. | x2-4+2x=(x+2)(x-2)+2x | ||
| C. | 2a(b-c)=2ab-2ac | D. | m2-n2=(m+n)(m-n) |
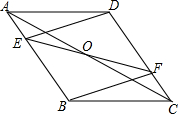 如图所示,O为?ABCD对角线AC的中点,EF经过点O交AB于E,交CD于点F,连接DE、BF.求证:四边形EBFD为平行四边形.
如图所示,O为?ABCD对角线AC的中点,EF经过点O交AB于E,交CD于点F,连接DE、BF.求证:四边形EBFD为平行四边形.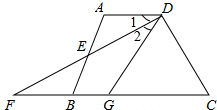 如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠1=∠2.
如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠1=∠2.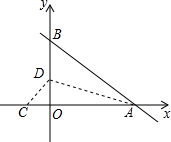 如图,在平面直角坐标系xOy中,直线y=-$\frac{4}{3}$x+3与x轴交于点A,与y轴交于点B,将△AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记作点C,折痕与y轴交于点D,则C、D两点的坐标分别为C (-$\frac{3}{2}$,0),D(0,$\frac{4}{3}$).
如图,在平面直角坐标系xOy中,直线y=-$\frac{4}{3}$x+3与x轴交于点A,与y轴交于点B,将△AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记作点C,折痕与y轴交于点D,则C、D两点的坐标分别为C (-$\frac{3}{2}$,0),D(0,$\frac{4}{3}$). 如图,AD是△ABC边BC上的高,BE平分∠ABC交AD于点E.若∠C=60°,∠BED=70°.求∠ABC和∠BAC的度数.
如图,AD是△ABC边BC上的高,BE平分∠ABC交AD于点E.若∠C=60°,∠BED=70°.求∠ABC和∠BAC的度数.