题目内容
4.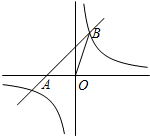 如图,一次函数y=x+2的图象交x轴于点A,且过点B(1,m).点B在反比例函数y=$\frac{k}{x}$(k≠0)的图象上.
如图,一次函数y=x+2的图象交x轴于点A,且过点B(1,m).点B在反比例函数y=$\frac{k}{x}$(k≠0)的图象上.(1)求该反比例函数的解析式;
(2)连结OB,求△AOB的面积;并结合图形直接写出当函数值y<m时,该反比例函数的自变量x的取值范围.
分析 (1)把B点坐标代入一次函数可求得m,可求得B点坐标,代入反比例函数解析式可求得k,可求得反比例函数解析式;
(2)可先求得A点的坐标,结合B点坐标可求得△AOB的面积;结合图象可知当函数值y<m时,即反比例函数图象在点B下方的部分对应的x的值,可得出x的范围.
解答 解:
(1)∵一次函数y=x+2的图象过点B(1,m),
∴m=1+2=3.
∴点B的坐标为(1,3).
∵点B在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,
∴3=$\frac{k}{1}$,即k=3.
∴该反比例函数的解析式为y=$\frac{3}{x}$.
(2)在y=x+2中,令y=0,则0=x+2,得x=-2,
∴点A的坐标为(-2,0),
∴OA=2.
又∵点B的坐标为(1,3),
∴△AOB中OA边上的高为3.
∴S△AOB=$\frac{1}{2}$×2×3=3,
当函数值y<m时,即y<3,由函数图象可知自变量x的取值范围是:x>1或x<0.
点评 本题主要考查反比例函数与一次函数的综合应用,在(1)中注意点的坐标与函数解析式的关系,在(2)中注意数形结合思想的应用.

练习册系列答案
相关题目
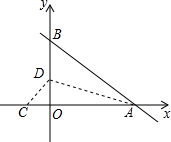 如图,在平面直角坐标系xOy中,直线y=-$\frac{4}{3}$x+3与x轴交于点A,与y轴交于点B,将△AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记作点C,折痕与y轴交于点D,则C、D两点的坐标分别为C (-$\frac{3}{2}$,0),D(0,$\frac{4}{3}$).
如图,在平面直角坐标系xOy中,直线y=-$\frac{4}{3}$x+3与x轴交于点A,与y轴交于点B,将△AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记作点C,折痕与y轴交于点D,则C、D两点的坐标分别为C (-$\frac{3}{2}$,0),D(0,$\frac{4}{3}$). 如图,AD是△ABC边BC上的高,BE平分∠ABC交AD于点E.若∠C=60°,∠BED=70°.求∠ABC和∠BAC的度数.
如图,AD是△ABC边BC上的高,BE平分∠ABC交AD于点E.若∠C=60°,∠BED=70°.求∠ABC和∠BAC的度数.

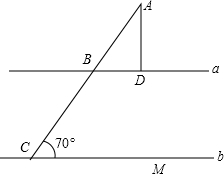 如图所示,已知a∥b,AD⊥直线a,求∠A的度数.
如图所示,已知a∥b,AD⊥直线a,求∠A的度数.