题目内容
9.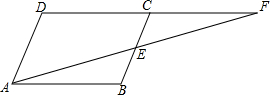 如图,在平行四边形ABCD中,E为BC的中点,AE的延长线与DC的延长线相交于F.
如图,在平行四边形ABCD中,E为BC的中点,AE的延长线与DC的延长线相交于F.①证明:∠DFA=∠FAB;
②证明:△ABE≌△FCE.
分析 (1)利用平行四边形的两组对边分别平行即可得到两角相等;
(2)利用上题证得的结论及平行四边形对边相等即可证明两三角形全等.
解答 证明:(1)∵四边形ABCD是平行四边形,
∴DF∥AB,
∴∠DFA=∠FAB;
(2)∵E为BC中点,
∴EC=EB,
∴在△ABE与△FCE中,
$\left\{\begin{array}{l}{∠DFA=∠FAB}\\{∠CEF=∠BEA}\\{EB=EC}\end{array}\right.$,
∴△ABE≌△FCE(AAS).
点评 此题主要考查平行四边形的性质和判定以及全等三角形的证明,使学生能够灵活运用平行四边形知识解决有关问题.

练习册系列答案
相关题目
19.三个连续自然数的和不大于15,这样的自然数组有( )
| A. | 3组 | B. | 4组 | C. | 5组 | D. | 6组 |
20.同一平面内,三条不同直线的交点个数可能是( )个.
| A. | 1或3 | B. | 0、1或3 | C. | 0、1或2 | D. | 0、1、2或3 |
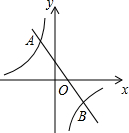 如图,在直角坐标系中,一次函数y=-x+b与反比例函数y=$\frac{-4}{x}$的图象交于A,B两点,已知A(-1,a).
如图,在直角坐标系中,一次函数y=-x+b与反比例函数y=$\frac{-4}{x}$的图象交于A,B两点,已知A(-1,a).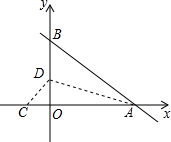 如图,在平面直角坐标系xOy中,直线y=-$\frac{4}{3}$x+3与x轴交于点A,与y轴交于点B,将△AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记作点C,折痕与y轴交于点D,则C、D两点的坐标分别为C (-$\frac{3}{2}$,0),D(0,$\frac{4}{3}$).
如图,在平面直角坐标系xOy中,直线y=-$\frac{4}{3}$x+3与x轴交于点A,与y轴交于点B,将△AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记作点C,折痕与y轴交于点D,则C、D两点的坐标分别为C (-$\frac{3}{2}$,0),D(0,$\frac{4}{3}$).