题目内容
10．已知方程组$\left\{\begin{array}{l}{ax+3by-c=0}\\{2ax-by-5c=0}\end{array}\right.$（abc≠0）的解是$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$，求a：b：c的值．分析 把方程组的解代入原方程组，用一个未知数表示出另外两个未知数的值，再代入所求代数式．
解答 解：把$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$，代入方程组$\left\{\begin{array}{l}{ax+3by-c=0}\\{2ax-by-5c=0}\end{array}\right.$，
得$\left\{\begin{array}{l}{a-6b-c=0①}\\{2a+2b-5c=0②}\end{array}\right.$，
②-①×2得：b=$\frac{3c}{14}$，
将b=$\frac{3c}{14}$代入①得：a=$\frac{16c}{7}$，
解得$\left\{\begin{array}{l}{a=\frac{16c}{7}}\\{b=\frac{3c}{14}}\end{array}\right.$．
所以a：b：c=$\frac{16}{7}c$：$\frac{3c}{14}$：c=32：3：14．
点评 本题考查了二元一次方程组的解，解答此题的关键是把一个未知数当做已知，表示出另外两个未知数，便可求解．
练习册系列答案
相关题目
一个长方体和圆柱体如图放置，长方体的宽度与圆柱直径相等，则下面左视图正确的是（ ）
1．
如图，P是⊙O外一点，PO交⊙O于C点，PA和PB分别切⊙O于A和B点，已知⊙O的半径为3cm，∠APB=60°．若用图中阴影部分的扇形围成一个圆锥的侧面，则这个圆锥的高为（ ）
如图，P是⊙O外一点，PO交⊙O于C点，PA和PB分别切⊙O于A和B点，已知⊙O的半径为3cm，∠APB=60°．若用图中阴影部分的扇形围成一个圆锥的侧面，则这个圆锥的高为（ ）| A． | 2$\sqrt{2}$cm | B． | $\sqrt{2}$cm | C． | $\sqrt{10}$cm | D． | $\frac{3}{2}$cm |
4．观察下列图形，阅读图形下面的相关文字，
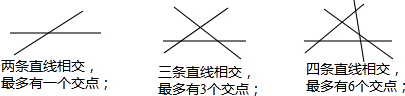
（1）填空
（2）当若干条直线相交时，设最多交点个数为m，对顶角对数为n，则m与n有何关系？
（1）填空
| 直线条数 | 最多交点个数 | 对顶角的对数 |
| 2 | 1 | 2 |
| 3 | 3 | 6 |
| 4 | 6 | 12 |
| 5 | 10 | 20 |
| … | … | … |
| n | $\frac{n（n-1）}{2}$ | n（n-1） |
