题目内容
11.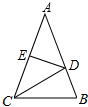 如图,在△ABC中,DE是AC的垂直平分线,分别交AB、AC于D、E两点.
如图,在△ABC中,DE是AC的垂直平分线,分别交AB、AC于D、E两点.(1)求证:△ACD是等腰三角形;
(2)若AE=5,△CBD的周长为24,求△ABC的周长.
分析 (1)根据线段的垂直平分线的性质得到DA=DC,证明结论;
(2)根据线段的垂直平分线的定义得到EC=EA=5,根据△CBD的周长为24,得到答案.
解答 (1)证明:∵DE是AC的垂直平分线,
∴DA=DC,
∴△ACD是等腰三角形;
(2)解:∵DE是AC的垂直平分线,
∴EC=EA=5,
∵△CBD的周长为24,
∴CB+BD+CD=24,
∴CB+AB=24,
∴△ABC的周长=AC+BC+AB=34.
点评 本题考查的是线段的垂直平分线的性质和等腰三角形的判定,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
相关题目
1.己知圆的半径分别为4厘米,圆心到一直线距离3厘米,则直线与圆的位置关系是( )
| A. | 相交 | B. | 相离 | C. | 相切 | D. | 内含 |
19.已知y=ax2+k的图象上有三点A(-3,y1),B(1,y2),C(2,y3),且y2<y3<y1,则a的取值范围是( )
| A. | a>0 | B. | a<0 | C. | a≥0 | D. | a≤0 |
6.下列说法正确的是( )
| A. | 两个数相加的和一定大于其中一个加数 | |
| B. | 两个有理数相加同号得正,异号得负 | |
| C. | 两个负数相加,和取负,并把绝对值相减 | |
| D. | 两个数相加的和可能为零 |
 用锤子以均匀的力敲铁钉进入木板,随着铁钉的进入,铁钉所受的阻力也会越来起大,设每次进入木板的钉子长度为前-次进人木板的长度的x,其中0<x<1(第一次除外),已知某人敲击第一次受敲击后进入木板部分的铁钉长度为钉长的$\frac{4}{7}$,某人敲击三次完全钉入木板中,求x的值.
用锤子以均匀的力敲铁钉进入木板,随着铁钉的进入,铁钉所受的阻力也会越来起大,设每次进入木板的钉子长度为前-次进人木板的长度的x,其中0<x<1(第一次除外),已知某人敲击第一次受敲击后进入木板部分的铁钉长度为钉长的$\frac{4}{7}$,某人敲击三次完全钉入木板中,求x的值.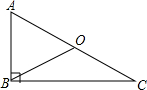 如图,已知Rt△ABC,∠ABC=90°,BO是斜边AC上的中线.
如图,已知Rt△ABC,∠ABC=90°,BO是斜边AC上的中线.