题目内容
14.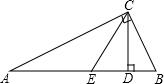 如图,在Rt△ABC中,已知∠ACB=90°,BC=2$\sqrt{3}$,CD⊥AB,垂足为点D,CD,CE三等分∠ACB,求△ACE的周长.
如图,在Rt△ABC中,已知∠ACB=90°,BC=2$\sqrt{3}$,CD⊥AB,垂足为点D,CD,CE三等分∠ACB,求△ACE的周长.
分析 通过已知条件可以求得∠ACE=∠ECD=∠BCD=30°,∠ECB=60°,由CD⊥AB,求得∠B=60°,则由直角三角形的两个锐角互余的性质得到∠A=30°,解直角三角形求得AB、AC,即可求得△ACE的周长.
解答 证明:∵∠ACB=90°,CD,CE三等分∠ACB,
∴∠ACE=∠ECD=∠BCD=30°,∠ECB=60°,
∵CD⊥AB,
∴∠B=60°,
∴∠A=30°,
∴AB=2BC=4$\sqrt{3}$,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=6,
∴△ACE的周长=AB+AC+BC=4$\sqrt{3}$+2$\sqrt{3}$+6=6$\sqrt{3}$+6.
点评 本题考查了等腰三角形的判定和性质以及解直角三角形等,求得∠A=30°是本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.北京奥运会火炬传递的总里程约130400000米,用科学记数法表示为( )米(保留3个有效数字)
| A. | 1.3×108 | B. | 1.30×108 | C. | 0.13×109 | D. | 1.304×108 |
19.已知y=ax2+k的图象上有三点A(-3,y1),B(1,y2),C(2,y3),且y2<y3<y1,则a的取值范围是( )
| A. | a>0 | B. | a<0 | C. | a≥0 | D. | a≤0 |
6.下列说法正确的是( )
| A. | 两个数相加的和一定大于其中一个加数 | |
| B. | 两个有理数相加同号得正,异号得负 | |
| C. | 两个负数相加,和取负,并把绝对值相减 | |
| D. | 两个数相加的和可能为零 |
 某养鸡场要用长100m的篱笆搭4间鸡舍,如图所示,其中一边靠墙(足够长).若设另一边篱笆的长为xm,则整个鸡舍的面积S(m2)与x(m)之间的函数解析式是-5x2+100x,鸡舍的最大面积为500m2.
某养鸡场要用长100m的篱笆搭4间鸡舍,如图所示,其中一边靠墙(足够长).若设另一边篱笆的长为xm,则整个鸡舍的面积S(m2)与x(m)之间的函数解析式是-5x2+100x,鸡舍的最大面积为500m2. 用锤子以均匀的力敲铁钉进入木板,随着铁钉的进入,铁钉所受的阻力也会越来起大,设每次进入木板的钉子长度为前-次进人木板的长度的x,其中0<x<1(第一次除外),已知某人敲击第一次受敲击后进入木板部分的铁钉长度为钉长的$\frac{4}{7}$,某人敲击三次完全钉入木板中,求x的值.
用锤子以均匀的力敲铁钉进入木板,随着铁钉的进入,铁钉所受的阻力也会越来起大,设每次进入木板的钉子长度为前-次进人木板的长度的x,其中0<x<1(第一次除外),已知某人敲击第一次受敲击后进入木板部分的铁钉长度为钉长的$\frac{4}{7}$,某人敲击三次完全钉入木板中,求x的值.