题目内容
1.在平面直角坐标系xOy中,直线AB交y轴于A点,交x轴于B点,A(0,6),B(6,0).(1)现在一直角三角板的直角顶点放置于AB的中点C,并绕C点旋转,两直角边分别交x轴、y轴于N、M(如图)两点,求证:CM=CN;
(2)已知点D(4,6),求点D关于直线AB对称的点的坐标;
(3)若E是线段OB上一点,∠AEO=67.5°,OF⊥AE于G,交AB于F,求$\frac{GE}{AE-OF}$的值.
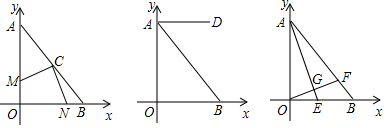
分析 (1)先连接OC,通过判定△OCM≌△BCN(ASA),即可得出CM=CN;
(2)过D作DD′⊥AB于H,交y轴于D′,根据AB为DD′的垂直平分线,即可得到D′为D点关于AB的对称点,再根据D(4,6),得到AD′=AD=4,进而得到OD′=6-4=2,最后得出D′(0,2);
(3)过B作BM⊥OF于M,则∠M=90°,通过判定△AOG≌△OBM(AAS),得到AG=OM,OG=BM,再判定△OGE≌△BFM(ASA),得到GE=FM,根据AE=AG+GE,OF=OM-FM,即可得到AE-OF=(AG+GE)-(OM-FM)=GE+FM=2GE,最后求得$\frac{GE}{AE-OF}$的值.
解答  解:(1)连接OC,
解:(1)连接OC,
∵OA=OB=6,C为AB的中点,
∴OC⊥AB,OC=AC=BC,
∴∠MOC=45°=∠NBC,
∵∠MCO+∠OCN=∠OCN+∠NCB=90°,
∴∠MCO=∠NCB,
在△OCM和△BCN中,
$\left\{\begin{array}{l}{∠MOC=∠NBC}\\{OC=BC}\\{∠MCO=∠NCB}\end{array}\right.$,
∴△OCM≌△BCN(ASA),
∴CM=CN;
(2)过D作DD′⊥AB于H,交y轴于D′,
∵∠OAB=45° ,
,
∴∠BAD=45°,
∵∠AHD=90°,
∴∠ADD′=45°,
∴AB为DD′的垂直平分线,
∴D′为D点关于AB的对称点,
∵D(4,6),
∴AD′=AD=4,
∴OD′=6-4=2,
∴D′(0,2);
(3)过B作BM⊥OF于M,则∠M=90°,
∵AE⊥OF,∠AOE=90°,
∴∠AGO=∠M=90°,∠OAG=∠BOM,
在△AOG和△OBM中,
$\left\{\begin{array}{l}{∠OAG=∠BOM}\\{AO=OB}\\{∠AGO=∠M}\end{array}\right.$,
∴△AOG≌△OBM(AAS),
∴AG=OM,OG=BM,
∵∠AEO=67.5°,OF⊥AE,∠AOE=90°,
∴∠EOG=22.5°=∠OAG,
又∵∠OAB=45°,
∴∠BAE=22.5°,
∵AE∥BM,
∴∠MBF=∠BAE=22.5°,
∴∠FBM=∠EOG,
在△OGE和△BFM中,
$\left\{\begin{array}{l}{∠OGE=∠M}\\{OG=BM}\\{∠FBM=∠EOG}\end{array}\right.$,
∴△OGE≌△BFM(ASA),
∴GE=FM,
∵AE=AG+GE,OF=OM-FM,
∴AE-OF=(AG+GE)-(OM-FM)=GE+FM=2GE,
∴$\frac{GE}{AE-OF}$=$\frac{GE}{2GE}$=$\frac{1}{2}$.
点评 本题属于三角形综合题,主要考查了全等三角形的判定与性质,线段垂直平分线的性质以及等腰直角三角形的性质的综合应用,解决问题的关键是作辅助线构造全等三角形,根据全等三角形的对应边相等进行推导计算.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
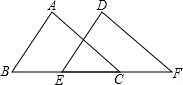 已知,∠ABC=∠DEF,AB=DE,要说明△ABC≌△DEF,若以“AAS”为依据,还要添加的条件为∠ACB=∠F.
已知,∠ABC=∠DEF,AB=DE,要说明△ABC≌△DEF,若以“AAS”为依据,还要添加的条件为∠ACB=∠F.