题目内容
7.在RT△ABC中,∠C=90°,BC=3cm,AC=4cm,以点C为圆心,以2.5cm为半径画圆,则⊙C与直线AB的位置关系是( )| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不能确定 |
分析 过C作CD⊥AB于D,根据勾股定理求出AB,根据三角形的面积公式求出CD,得出d<r,根据直线和圆的位置关系即可得出结论.
解答 解:过C作CD⊥AB于D,如图所示: ∵在Rt△ABC中,∠C=90°,AC=4,BC=3,
∵在Rt△ABC中,∠C=90°,AC=4,BC=3,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,
∵△ABC的面积=$\frac{1}{2}$AC×BC=$\frac{1}{2}$AB×CD,
∴3×4=5CD,
∴CD=2.4<2.5,
即d<r,
∴以2.5为半径的⊙C与直线AB的关系是相交;
故选A.
点评 本题考查了直线和圆的位置关系,用到的知识点是勾股定理,三角形的面积公式;解此题的关键是能正确作出辅助线,并进一步求出CD的长,注意:直线和圆的位置关系有:相离,相切,相交.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列说法错误的是( )
| A. | 对角线互相平分的四边形是平行四边形 | |
| B. | 两组对边分别相等的四边形是平行四边形 | |
| C. | 一组对边平行且相等的四边形是平行四边形 | |
| D. | 一组对边相等,另一组对边平行的四边形是平行四边形 |
12.4的平方根是( )
| A. | 2 | B. | -2 | C. | ±$\sqrt{2}$ | D. | ±2 |

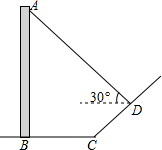 如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)
如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号) 如图,直线y=$\sqrt{3}$x+$\sqrt{3}$与两坐标轴分别交于A、B两点.
如图,直线y=$\sqrt{3}$x+$\sqrt{3}$与两坐标轴分别交于A、B两点.