题目内容
16.解方程组$\left\{\begin{array}{l}{9{x}^{2}-4{y}^{2}=36}\\{x-y=2}\end{array}\right.$.分析 首先联立方程组消去x求出y的值,然后再把y的值代入x-y=2中求出x的值即可.
解答 解:将两式联立消去x得:
9(y+2)2-4y2=36,
即5y2+36y=0,
解得:y=0或-$\frac{36}{5}$,
当y=0时,x=2,
y=-$\frac{36}{5}$时,x=-$\frac{26}{5}$;
原方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{26}{5}}\\{y=-\frac{36}{5}}\end{array}\right.$.
点评 本题主要考查了高次方程的知识,解答本题的关键是进行降次解方程,此题难度不大.

练习册系列答案
相关题目
7.在RT△ABC中,∠C=90°,BC=3cm,AC=4cm,以点C为圆心,以2.5cm为半径画圆,则⊙C与直线AB的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不能确定 |
4.$\frac{1}{2}$的倒数是( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -2 | D. | -$\frac{1}{2}$ |
8.不等式组$\left\{\begin{array}{l}{x-1>1}\\{x+8<4x-1}\end{array}\right.$的解集是( )
| A. | x>3 | B. | x<3 | C. | x<2 | D. | x>2 |
 如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm. 如图所示,一只蚂蚁从A点出发到D,E,F处寻觅食物.假定蚂蚁在每个岔路口都等可能的随机选择一条向左下或右下的路径(比如A岔路口可以向左下到达B处,也可以向右下到达C处,其中A,B,C都是岔路口).那么,蚂蚁从A出发到达E处的概率是$\frac{1}{2}$.
如图所示,一只蚂蚁从A点出发到D,E,F处寻觅食物.假定蚂蚁在每个岔路口都等可能的随机选择一条向左下或右下的路径(比如A岔路口可以向左下到达B处,也可以向右下到达C处,其中A,B,C都是岔路口).那么,蚂蚁从A出发到达E处的概率是$\frac{1}{2}$.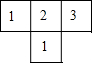 如图是由几个大小相同的小正方体搭成的几何体的俯视图,小正方形中数字表示该位置小正方体的个数,则该几何体的左视图是( )
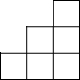
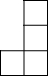
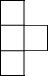
如图是由几个大小相同的小正方体搭成的几何体的俯视图,小正方形中数字表示该位置小正方体的个数,则该几何体的左视图是( )
 如图,在平面直角坐标系中,已知抛物线y=ax2+bx的对称轴为x=$\frac{3}{4}$,且经过点A(2,1),点P是抛物线上的动点,其横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,交OA于点C.点O关于直线PB的对称点为D,连接CD、AD,过点A作AE⊥x轴,垂足为E.
如图,在平面直角坐标系中,已知抛物线y=ax2+bx的对称轴为x=$\frac{3}{4}$,且经过点A(2,1),点P是抛物线上的动点,其横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,交OA于点C.点O关于直线PB的对称点为D,连接CD、AD,过点A作AE⊥x轴,垂足为E.