题目内容
17. 如图,直线y=$\sqrt{3}$x+$\sqrt{3}$与两坐标轴分别交于A、B两点.
如图,直线y=$\sqrt{3}$x+$\sqrt{3}$与两坐标轴分别交于A、B两点.(1)求∠ABO的度数;
(2)过A的直线l交x轴正半轴于C,AB=AC,求直线l的函数解析式.
分析 (1)根据函数解析式求出点A、B的坐标,然后在Rt△ABO中,利用三角函数求出tan∠ABO的值,继而可求出∠ABO的度数;
(2)根据题意可得,AB=AC,AO⊥BC,可得AO为BC的中垂线,根据点B的坐标,得出点C的坐标,然后利用待定系数法求出直线l的函数解析式.
解答 解:(1)对于直线y=$\sqrt{3}$x+$\sqrt{3}$,
令x=0,则y=$\sqrt{3}$,
令y=0,则x=-1,
故点A的坐标为(0,$\sqrt{3}$),点B的坐标为(-1,0),
则AO=$\sqrt{3}$,BO=1,
在Rt△ABO中,
∵tan∠ABO=$\frac{AO}{BO}$=$\sqrt{3}$,
∴∠ABO=60°;
(2)在△ABC中,
∵AB=AC,AO⊥BC,
∴AO为BC的中垂线,
即BO=CO,
则C点的坐标为(1,0),
设直线l的解析式为:y=kx+b(k,b为常数),
则$\left\{\begin{array}{l}{\sqrt{3}=b}\\{0=k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\sqrt{3}}\\{b=\sqrt{3}}\end{array}\right.$,
即函数解析式为:y=-$\sqrt{3}$x+$\sqrt{3}$.
点评 本题考查了待定系数法求一次函数解析式,涉及了的知识点有:待定系数法确定一次函数解析式,一次函数与坐标轴的交点,坐标与图形性质,熟练掌握待定系数法是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.在RT△ABC中,∠C=90°,BC=3cm,AC=4cm,以点C为圆心,以2.5cm为半径画圆,则⊙C与直线AB的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不能确定 |
8.不等式组$\left\{\begin{array}{l}{x-1>1}\\{x+8<4x-1}\end{array}\right.$的解集是( )
| A. | x>3 | B. | x<3 | C. | x<2 | D. | x>2 |
9.近几年来,我市加大教育信息化投入,投资201000000元,初步完成咸宁市教育公共云服务平台基础工程,教学点数字教育资源全覆盖,将201000000用科学记数法表示为( )
| A. | 20.1×107 | B. | 2.01×108 | C. | 2.01×109 | D. | 0.201×1010 |
15.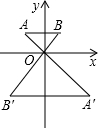 如图,已知△OAB与△OA′B′是相似比为 1:2 的位似图形,点O为位似中心,若△OAB内一点P(x,y)与△OA′B′内一点P′是一对对应点,则点P′的坐标为( )
如图,已知△OAB与△OA′B′是相似比为 1:2 的位似图形,点O为位似中心,若△OAB内一点P(x,y)与△OA′B′内一点P′是一对对应点,则点P′的坐标为( )
 如图,已知△OAB与△OA′B′是相似比为 1:2 的位似图形,点O为位似中心,若△OAB内一点P(x,y)与△OA′B′内一点P′是一对对应点,则点P′的坐标为( )
如图,已知△OAB与△OA′B′是相似比为 1:2 的位似图形,点O为位似中心,若△OAB内一点P(x,y)与△OA′B′内一点P′是一对对应点,则点P′的坐标为( )| A. | (-x,-y) | B. | (-2x,-2y) | C. | (-2x,2y) | D. | (2x,-2y) |
 如图,在平面直角坐标系中,已知抛物线y=ax2+bx的对称轴为x=$\frac{3}{4}$,且经过点A(2,1),点P是抛物线上的动点,其横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,交OA于点C.点O关于直线PB的对称点为D,连接CD、AD,过点A作AE⊥x轴,垂足为E.
如图,在平面直角坐标系中,已知抛物线y=ax2+bx的对称轴为x=$\frac{3}{4}$,且经过点A(2,1),点P是抛物线上的动点,其横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,交OA于点C.点O关于直线PB的对称点为D,连接CD、AD,过点A作AE⊥x轴,垂足为E.