题目内容
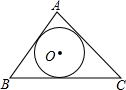已知，如图，在锐角△ABC中，tanB=| 3 |
| 4 |
考点：三角形的内切圆与内心
专题：
分析：过点A作AD⊥BC，根据tanB=
，可求得AD和BD，再根据勾股定理得出AC，再把三角形ABC的面积分成三个三角形的面积，即可求得△ABC的内切圆O的半径．
| 3 |
| 4 |
解答：解：
过点A作AD⊥BC，设圆O半径为r，
∵tanB=
，
∴
=
，
在Rt△ABD中，AD2+BD2=AB2，
∵AB=5，BC=6，
∴AD=3，BD=4
∴CD=2，
∴由勾股定理得AC=
，
S△ABC=S△AOB+S△AOC+S△BOC，
BD•AD=AB•r+AC•r+BC•r
12=5r+
r+6r，
解得r=
．
过点A作AD⊥BC，设圆O半径为r，∵tanB=
| 3 |
| 4 |
∴
| AD |
| BD |
| 3 |
| 4 |
在Rt△ABD中，AD2+BD2=AB2，
∵AB=5，BC=6，
∴AD=3，BD=4
∴CD=2，
∴由勾股定理得AC=
| 13 |
S△ABC=S△AOB+S△AOC+S△BOC，
BD•AD=AB•r+AC•r+BC•r
12=5r+
| 13 |
解得r=
11-
| ||
| 9 |
点评：本题考查了三角形的内切圆与内心，以及勾股定理、三角形的面积公式，是中档题，难度不大．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
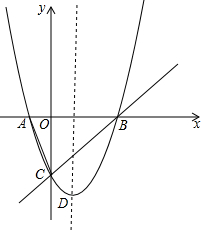如图所示，抛物线y=x2-2x-3的图象与x轴交于A，B两点，与y轴交于C点，顶点为D，直线y=x-3经过点B，C，连接AC． 
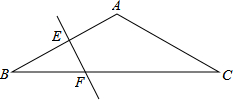在△ABBC中，AB=AC，∠BAC=120°，EF为AB的垂直平分线，求证：BF=
如图，点A和点B分别是棱长为20cm的正方体盒子上两条棱的中点，一只昆虫沿盒子的表面由A处爬行到B处，所走的最短路程是多少？若b是方程bx+ax+b=0的一个解，且b≠0，则a+b等于（ ）
| A、-1 | B、1 | C、-2 | D、2 |