题目内容
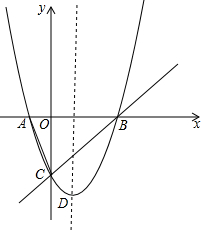 如图所示,抛物线y=x2-2x-3的图象与x轴交于A,B两点,与y轴交于C点,顶点为D,直线y=x-3经过点B,C,连接AC.
如图所示,抛物线y=x2-2x-3的图象与x轴交于A,B两点,与y轴交于C点,顶点为D,直线y=x-3经过点B,C,连接AC. (1)求tan∠ACO;
(2)在直线BC下方的抛物线上有一点M,使得四边形ABMC面积最大,求点M的坐标并写出四边形ABMC面积的最大值;
(3)点H在抛物线上,当∠HBC=∠ACO时,求点H的坐标.
考点:二次函数综合题
专题:压轴题
分析:(1)令y=0,解方程得到点A、B的坐标,令x=0求出点C的坐标,然后根据锐角三角函数的正切等于对边比邻边列式即可;
(2)先求出△ABC的面积,然后判断出△BCM的面积最大时四边形ABMC面积最大,求出直线BC的解析式,设过点M与y轴平行的直线与BC相交于点N,表示出MN,再表示出△BCM的面积,然后利用二次函数的最值问题求出点M的横坐标以及△BCM的面积,最后求解即可;
(3)求出点D的坐标,然后求出∠BCD=90°,再求出∠CBD的正切值,得到∠DBC=∠ACO,从而确定出点H与点D重合,再求出点D关于点C的对称点D′,再求出直线BD′的解析式,然后与抛物线解析式联立求解即可.
(2)先求出△ABC的面积,然后判断出△BCM的面积最大时四边形ABMC面积最大,求出直线BC的解析式,设过点M与y轴平行的直线与BC相交于点N,表示出MN,再表示出△BCM的面积,然后利用二次函数的最值问题求出点M的横坐标以及△BCM的面积,最后求解即可;
(3)求出点D的坐标,然后求出∠BCD=90°,再求出∠CBD的正切值,得到∠DBC=∠ACO,从而确定出点H与点D重合,再求出点D关于点C的对称点D′,再求出直线BD′的解析式,然后与抛物线解析式联立求解即可.
解答:解:(1)令y=0,则x2-2x-3=0,
解得x1=-1,x2=3,
所以,点A(-1,0),B(3,0),
令x=0,则y=-3,
所以,点C的坐标为(0,-3),
所以,tan∠ACO=
=
;
(2)∵AB=3-(-1)=4,OC=3,
∴S△ABC=
AB•OC=
×4×3=6,
所以,△BCM的面积最大时四边形ABMC面积最大,
设直线BC的解析式为y=kx+b,
则
,
解得
,
所以,直线BC的解析式为y=x-3,
设过点M与y轴平行的直线与BC相交于点N,
则MN=(x-3)-(x2-2x-3)=-x2+3x,
S△BCM=
(-x2+3x)×3=-
(x-
)2+
,
∵a=-
,
∴当x=
时,△BCM的面积最大,最大值为
,
此时,y=(
)2-2×
-3=-
,
所以,当点M(
,-
)时,四边形ABMC面积最大,最大值为6+
=
;
(3)①∵y=x2-2x-3=(x-1)2-4,
∴顶点D的坐标为(1,-4),
∵B(3,0),C(0,-3),
∴∠BCO=45°,CD与y轴的夹角为45°,
∴∠BCD=90°,
∵BC=
=3
,CD=
=
,
∴tan∠CBD=
=
,
∴∠DBC=∠ACO,
∴点H与点D重合,
故,点H的坐标为(1,-4),
②∵点D(1,-4),C(0,-3),
∴点D关于点C的对称点D′(-1,-2),
设直线BD′的解析式为y=mx+n,
则
,
解得
,
所以,直线BD′的解析式为y=
x-
,
联立
,
解得
(为点B坐标,舍去),
,
所以,点H的坐标为(-
,-
),
综上所述,点H的坐标为(1,-4)或(-
,-
)时,∠HBC=∠ACO.
解得x1=-1,x2=3,
所以,点A(-1,0),B(3,0),
令x=0,则y=-3,
所以,点C的坐标为(0,-3),
所以,tan∠ACO=
| AO |
| CO |
| 1 |
| 3 |
(2)∵AB=3-(-1)=4,OC=3,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
所以,△BCM的面积最大时四边形ABMC面积最大,

设直线BC的解析式为y=kx+b,
则
|
解得
|
所以,直线BC的解析式为y=x-3,
设过点M与y轴平行的直线与BC相交于点N,
则MN=(x-3)-(x2-2x-3)=-x2+3x,
S△BCM=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 27 |
| 8 |
∵a=-
| 1 |
| 2 |
∴当x=
| 3 |
| 2 |
| 27 |
| 8 |
此时,y=(
| 3 |
| 2 |
| 3 |
| 2 |
| 15 |
| 4 |
所以,当点M(
| 3 |
| 2 |
| 15 |
| 4 |
| 27 |
| 8 |
| 75 |
| 8 |
(3)①∵y=x2-2x-3=(x-1)2-4,
∴顶点D的坐标为(1,-4),
∵B(3,0),C(0,-3),
∴∠BCO=45°,CD与y轴的夹角为45°,
∴∠BCD=90°,
∵BC=
| 32+32 |
| 2 |
| 12+(-3+4)2 |
| 2 |
∴tan∠CBD=
| ||
3
|
| 1 |
| 3 |
∴∠DBC=∠ACO,
∴点H与点D重合,
故,点H的坐标为(1,-4),
②∵点D(1,-4),C(0,-3),
∴点D关于点C的对称点D′(-1,-2),
设直线BD′的解析式为y=mx+n,
则
|
解得
|
所以,直线BD′的解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
联立
|
解得
|
|
所以,点H的坐标为(-
| 1 |
| 2 |
| 7 |
| 4 |
综上所述,点H的坐标为(1,-4)或(-
| 1 |
| 2 |
| 7 |
| 4 |
点评:本题是二次函数综合题型,主要利用了二次函数与坐标轴的交点坐标的求法,待定系数法求一次函数解析式,二次函数的最值问题,难点在于(3)先判断出顶点坐标D为所求的点H之一.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
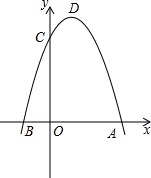 如图,二次函数y=-x2+2(m-2)x+3的图象与x,y轴交于A,B,C三点,其中A(3,0),抛物线的顶点为D.
如图,二次函数y=-x2+2(m-2)x+3的图象与x,y轴交于A,B,C三点,其中A(3,0),抛物线的顶点为D.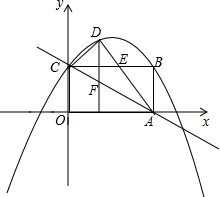 已知一个矩形纸片OABC,将该纸片放置在平面直角坐标系中,如图,点A(5,0),从(0,
已知一个矩形纸片OABC,将该纸片放置在平面直角坐标系中,如图,点A(5,0),从(0,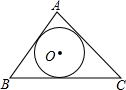 已知,如图,在锐角△ABC中,tanB=
已知,如图,在锐角△ABC中,tanB= 如图所示,在平面直角坐标系中,矩形OABC的对角线AC=10,OA、OC是方程x2-2(k+3)+12k=0的两根,且OA>OC,点D在BC上,直线l平分矩形OABC的面积.
如图所示,在平面直角坐标系中,矩形OABC的对角线AC=10,OA、OC是方程x2-2(k+3)+12k=0的两根,且OA>OC,点D在BC上,直线l平分矩形OABC的面积.