题目内容
20.已知抛物线y=ax2+bx+c(a>0)过(-2,0),(2,3)两点,那么抛物线的对称轴( )| A. | 只能是x=-1 | B. | 可能是y轴 | ||
| C. | 在y轴右侧且在直线x=2的左侧 | D. | 在y轴左侧 |
分析 根据题意判定点(-2,0)关于对称轴的对称点横坐标x2满足:-2<x2<2,从而得出-2<$\frac{{x}_{1}+{x}_{2}}{2}$<0,即可判定抛物线对称轴的位置.
解答 解:∵抛物线y=ax2+bx+c(a>0)过(-2,0),(2,3)两点,
∴点(-2,0)关于对称轴的对称点横坐标x2满足:-2<x2<2,
∴-2<$\frac{{x}_{1}+{x}_{2}}{2}$<0,
∴抛物线的对称轴可能在y轴左侧且在直线x=-2的右侧.
故选:C.
点评 本题考查了二次函数的性质,根据点坐标判断出另一个点的位置是解题的关键.

练习册系列答案
相关题目
10.在函数$y=\frac{x-1}{{\sqrt{4-x}}}$中,自变量x的取值范围是( )
| A. | x≠4 | B. | x≤4 | C. | x<4 | D. | 1<x<4 |
8.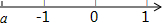 有理数a在数轴上对应的点如图所示,则a,-a,1的大小关系正确的是( )
有理数a在数轴上对应的点如图所示,则a,-a,1的大小关系正确的是( )
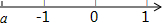 有理数a在数轴上对应的点如图所示,则a,-a,1的大小关系正确的是( )
有理数a在数轴上对应的点如图所示,则a,-a,1的大小关系正确的是( )| A. | -a<a<1 | B. | a<-a<1 | C. | 1<-a<a | D. | a<1<-a |
10.式子-mn与(-m)n的正确判断是( )
| A. | 这两个式子互为相反数 | B. | 这两个式子是相等的 | ||
| C. | 当n为奇数时,它们相等 | D. | n为偶数时它们相等 |