题目内容
9.化简:($\frac{1}{{a}^{2}-a+1}$-$\frac{1-a}{{a}^{3}-1}$)÷$\frac{{a}^{4}-{a}^{2}-2}{({a}^{6}-1)-({a}^{4}+{a}^{2}+1)}$.分析 利用立方差公式和十字相乘法对分式的分子、分母因式分解,根据分式的混合运算顺序逐一进行即可.
解答 解:原式=[$\frac{1}{{a}^{2}-a+1}$+$\frac{a-1}{(a-1)({a}^{2}+a+1)}$]÷$\frac{({a}^{2}+1)({a}^{2}-2)}{({a}^{2}-1)({a}^{4}+{a}^{2}+1)-({a}^{4}+{a}^{2}+1)}$
=($\frac{1}{{a}^{2}+1-a}$+$\frac{1}{{a}^{2}+1+a}$)÷$\frac{({a}^{2}+1)({a}^{2}-2)}{({a}^{4}+{a}^{2}+1)({a}^{2}-2)}$
=$\frac{{a}^{2}+1+a+{a}^{2}+1-a}{({a}^{2}+1)^{2}-{a}^{2}}$•$\frac{{a}^{4}+{a}^{2}+1}{{a}^{2}+1}$
=$\frac{2({a}^{2}+1)}{{a}^{4}+{a}^{2}+1}$•$\frac{{a}^{4}+{a}^{2}+1}{{a}^{2}+1}$
=2.
点评 本题主要考查分式的混合运算,熟练掌握立方差公式和十字相乘法对分子、分母因式分解及分式的混合运算顺序是解题的关键.

练习册系列答案
相关题目
20.已知抛物线y=ax2+bx+c(a>0)过(-2,0),(2,3)两点,那么抛物线的对称轴( )
| A. | 只能是x=-1 | B. | 可能是y轴 | ||
| C. | 在y轴右侧且在直线x=2的左侧 | D. | 在y轴左侧 |
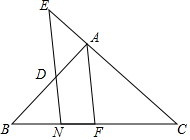 如图,在△ABC中,直线DN平行于中线AF交AB于点D,交AC的延长线于点E,交边BC于点N,求证:$\frac{AD}{AB}$=$\frac{AE}{AC}$.
如图,在△ABC中,直线DN平行于中线AF交AB于点D,交AC的延长线于点E,交边BC于点N,求证:$\frac{AD}{AB}$=$\frac{AE}{AC}$.