题目内容
15．已知关于x、y的方程组$\left\{\begin{array}{l}{mx-\frac{1}{2}ny=\frac{1}{2}}\\{mx+ny=5}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$，求m、n的值．分析 把x与y的值代入方程组得出关于m、n的二元一次方程组，求得方程组的解即可．
解答 解：∵关于x、y的方程组$\left\{\begin{array}{l}{mx-\frac{1}{2}ny=\frac{1}{2}}\\{mx+ny=5}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$，
∴$\left\{\begin{array}{l}{2m-\frac{3}{2}n=\frac{1}{2}}\\{2m+3n=5}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{m=1}\\{n=1}\end{array}\right.$，
即m=1，n=1．
点评 此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程都成立的未知数的值，以及解二元一次方程组的方法．
练习册系列答案
53天天练系列答案
相关题目
12．下列表述中的数为准确数的是（ ）
| A． | 七年级有440名学生 | B． | 月球离地球的距离约为38万千米 | ||
| C． | 小明同学身高大约143cm | D． | 估计今天气温为26℃ |
13．下列说法中正确的有（ ）
（1）两点确定一条直线；
（2）射线AB和射线BA是同一条射线；
（3）若P点是线段AB中点，则AP=BP；
（4）连接两点的线段叫做两点间的距离．
（1）两点确定一条直线；
（2）射线AB和射线BA是同一条射线；
（3）若P点是线段AB中点，则AP=BP；
（4）连接两点的线段叫做两点间的距离．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
3．
我们曾经通过列表、画图象，研究了函数y=ax2（a≠0）的性质，知道它的图象是一条抛物线，通过图象还研究了它的相关性质；经过平移函数y=ax2（a≠0）的图象还可得到函数y=a（x-h）2+k，（a≠0）的图象．用类似的方法还可研究其他函数的有关性质．
下面请你通过类比，尝试研究一下函数y=$\frac{1}{2}$x3的性质：
（1）完成下表：
（2）在所给坐标系中作出函数y=$\frac{1}{2}$x3的图象；
（3）观察你画的函数y=$\frac{1}{2}$x3的图象，回答下列问题：
①函数y=$\frac{1}{2}$x3图象的对称性下列说法正确的是C．
A．关于x轴对称 B．关于y轴对称
C．关于原点对称 D．既不是轴对称也不是中心对称
②随x的增大，y有怎样的变化？
③y是否有最大或最小值？
④将函数y=$\frac{1}{2}$x3的图象向左平移一个单位，再向上平移两个单位．可得到怎样的函数表达式，请直接将你的猜想写出来？
我们曾经通过列表、画图象，研究了函数y=ax2（a≠0）的性质，知道它的图象是一条抛物线，通过图象还研究了它的相关性质；经过平移函数y=ax2（a≠0）的图象还可得到函数y=a（x-h）2+k，（a≠0）的图象．用类似的方法还可研究其他函数的有关性质．下面请你通过类比，尝试研究一下函数y=$\frac{1}{2}$x3的性质：
（1）完成下表：
| x | … | -2 | -1 | 0 | 1 | 2 | … | ||
| y | … | 0 | 4 | … |
（3）观察你画的函数y=$\frac{1}{2}$x3的图象，回答下列问题：
①函数y=$\frac{1}{2}$x3图象的对称性下列说法正确的是C．
A．关于x轴对称 B．关于y轴对称
C．关于原点对称 D．既不是轴对称也不是中心对称
②随x的增大，y有怎样的变化？
③y是否有最大或最小值？
④将函数y=$\frac{1}{2}$x3的图象向左平移一个单位，再向上平移两个单位．可得到怎样的函数表达式，请直接将你的猜想写出来？
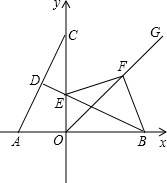如图，在直角坐标系中，A在x轴负半轴上，C点在y轴正半轴上，OG是第一象限角平分线，AC的垂直平分线分别与AC，y轴及x轴相交于D，E，B，且OC=OB