题目内容
8.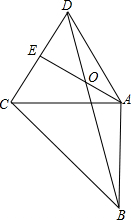 如图,△ACD是等边三角形,AE⊥CD于E,AB⊥AC,AC=AB,AE、BD相交于O.
如图,△ACD是等边三角形,AE⊥CD于E,AB⊥AC,AC=AB,AE、BD相交于O.(1)求∠ADB的度数;
(2)求证:BC=2OD.
分析 (1)由等边三角形和等腰直角三角形的性质得到∠DAB=150°AD=AC=AB,于是得到结论;
(2)由(1)的结论进而得出∠EDO=45°,即可得出△DEO是等腰直角三角形,求得AC=2ED,进而求得BC=2OD.
解答 解:(1)∵△ACD为等边三角形,△ABC是等腰直角三角形,
∴CD=AC=AD=AB,∠ADC=∠DAC=60°,∠CAB=90°,
∴∠BAD=150°,△ABD是等腰三角形,
∴∠ADB=15°;
(2)由(1)知∠ADB=15°,
∴∠EDO=45°,
又∵在等边三角形ACD中,AD=AC,AE⊥CD,
∴ED=$\frac{1}{2}$CD,且∠DEO=90°,
∴△DEO是等腰直角三角形,ED=$\frac{1}{2}$AC,
∴△DEO∽△BAC,
∴$\frac{BC}{OD}=\frac{AC}{DE}=2$.
∴BC=2OD.
点评 本题主要考查了等边三角形,等腰直角三角形的性质,相似三角形的判定和性质,熟练掌握各性质定理是解题的关键.

练习册系列答案
相关题目
19.下列因式分解中,正确的是( )
| A. | -2x3+6x2-2x=-2x(x2-3x-1) | B. | x2-3x+2=x(x-3)+2 | ||
| C. | 4x2-9=(2x-3)2 | D. | -x2+4xy-4y2=-(x-2y)2 |
16.在△ABC中,PA=PB=PC,则点P是△ABC( )
| A. | 三条角平分线的交点 | B. | 三边垂直平分线的交点 | ||
| C. | 三条中线的交点 | D. | 三条高的交点 |
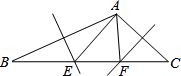 如图,△ABC中,∠BAC=110°,AB、CD的垂直平分线分别交BC于点E、F,则∠EAF的度数为40°.
如图,△ABC中,∠BAC=110°,AB、CD的垂直平分线分别交BC于点E、F,则∠EAF的度数为40°.