题目内容
19.已知x=$\frac{1}{2+\sqrt{3}}$,y=$\frac{1}{2-\sqrt{3}}$,求下列代数式的值:(1)x2+2xy+y2;
(2)x2-y2.
分析 首先化简x、y,再进一步(1)利用完全平方公式因式分解;(2)利用平方差公式因式分解;最后代入求得答案即可.
解答 解:x=$\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$,y=$\frac{1}{2-\sqrt{3}}$=2+$\sqrt{3}$,
(1)原式=(x+y)2=16;
(2)原式=(x+y)(x-y)=-8$\sqrt{3}$.
点评 此题考查二次根式的化简求值,注意先化简,再进一步代入求得数值即可.

练习册系列答案
相关题目
12.某旅游区,为美化地面,选用同样规格的黑白两色的正方形瓷砖铺设而成矩形地面,观察图形,请回答:第n个图中共有( )块瓷砖.
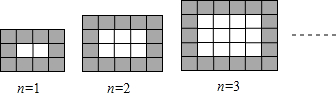

| A. | n2+6n+5 | B. | n2+5n+6 | C. | n2-6n+5 | D. | n2+5n-6 |
7.如图是用火柴棍摆成的边长分别是1、2、3根火柴棍时的正方形,当边长为6根火柴棍时,摆出的正方形所用的火柴棍的根数为( )


| A. | 60 | B. | 84 | C. | 96 | D. | 112 |
14.代数式$\frac{4x}{5}$,$\frac{4}{x+2y}$,$\frac{{x}^{2}+2}{π+1}$,$\frac{5}{2}$,$\frac{1}{b}$,2x+$\frac{1}{x}$中,是分式的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
4.已知圆外一点和圆周的最短距离为2,最长距离为8,则该圆的半径是( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
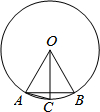 如图,在⊙O中,OA=AB,OC⊥AB,则下列结论正确的有A,B,D,F (填字母)
如图,在⊙O中,OA=AB,OC⊥AB,则下列结论正确的有A,B,D,F (填字母) 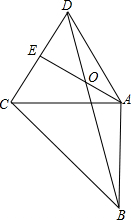 如图,△ACD是等边三角形,AE⊥CD于E,AB⊥AC,AC=AB,AE、BD相交于O.
如图,△ACD是等边三角形,AE⊥CD于E,AB⊥AC,AC=AB,AE、BD相交于O.