题目内容
已知a、b互为相反数,c、d互为倒数,|x-1|=1,则代数式x2-(a+b-cd)x+(-cd)2013的值等于( )
| A、5 | B、1 |
| C、1或-1 | D、5或-1 |
考点:代数式求值,相反数,绝对值,倒数
专题:
分析:根据相反数,绝对值,倒数的概念和性质求得a与b,c与d及x的关系或值后,代入代数式求值.
解答:解:∵a,b互为相反数,
∴a+b=0,
∵c,d互为倒数,
∴cd=1,
∵|x-1|=1,∴x=0或2,
当x=0时,
x2-(a+b-cd)x+(-cd)2013=0-0+(-1)2013=-1;
当x=2时,
x2-(a+b-cd)x+(-cd)2013=4-(0-1)×2+(-1)2013=5.
故代数式x2-(a+b-cd)x+(-cd)2013的值等于-1或5.
故选:D.
∴a+b=0,
∵c,d互为倒数,
∴cd=1,
∵|x-1|=1,∴x=0或2,
当x=0时,
x2-(a+b-cd)x+(-cd)2013=0-0+(-1)2013=-1;
当x=2时,
x2-(a+b-cd)x+(-cd)2013=4-(0-1)×2+(-1)2013=5.
故代数式x2-(a+b-cd)x+(-cd)2013的值等于-1或5.
故选:D.
点评:本题主要考查相反数,绝对值,倒数的概念及性质.
(1)相反数的定义:只有符号不同的两个数互为相反数,0的相反数是0;
(2)倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数;
(3)绝对值规律总结:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
(1)相反数的定义:只有符号不同的两个数互为相反数,0的相反数是0;
(2)倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数;
(3)绝对值规律总结:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.

练习册系列答案
相关题目
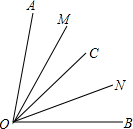 从点O发出的三条射线OA、OB、OC,其中∠AOB=80°,OM、ON分别平分∠AOC,∠BOC.
从点O发出的三条射线OA、OB、OC,其中∠AOB=80°,OM、ON分别平分∠AOC,∠BOC.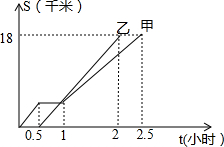 甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系的图象如图所示,下列说法:
甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系的图象如图所示,下列说法: 如图,A、B、C、D在同一直线上,AB=CD,DE∥AF,且DE=AF,那么△AFC≌△DEB成立吗?请说明你判别的理由.
如图,A、B、C、D在同一直线上,AB=CD,DE∥AF,且DE=AF,那么△AFC≌△DEB成立吗?请说明你判别的理由. 四张不透明的卡片,除正面分别有数字1、1、2、-3外,其他均相同,将这四张卡背面朝上洗均后放置在桌面上.
四张不透明的卡片,除正面分别有数字1、1、2、-3外,其他均相同,将这四张卡背面朝上洗均后放置在桌面上.