题目内容
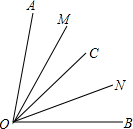 从点O发出的三条射线OA、OB、OC,其中∠AOB=80°,OM、ON分别平分∠AOC,∠BOC.
从点O发出的三条射线OA、OB、OC,其中∠AOB=80°,OM、ON分别平分∠AOC,∠BOC.(1)如图,射线OC落在∠AOB的内部,求∠MON的度数;
(2)当射线OC落在∠AOB的外部时,画出图形,求∠MON的度数.
(3)在(2)的条件下,当∠AOB=α,求∠MON的度数(直接写出结果).
考点:角的计算,角平分线的定义
专题:计算题
分析:(1)由OM,ON分别为∠AOC与∠BOC的角平分线,利用角平分线定义得到∠MOC=
∠AOC,∠NOC=
∠BOC,根据∠MON=∠MOC+∠NOC,等量代换即可求出度数;
(2)反向延长OA,OB到G,H,分三种情况考虑:(i)当OC落在∠AOH内时;(ii)当OC落在∠BOG内时;(iii)当OC落在∠HOG内时,分别求出∠MON的度数即可;
(3)根据(2)中的结论,归纳总结表示出∠MON的度数即可.
| 1 |
| 2 |
| 1 |
| 2 |
(2)反向延长OA,OB到G,H,分三种情况考虑:(i)当OC落在∠AOH内时;(ii)当OC落在∠BOG内时;(iii)当OC落在∠HOG内时,分别求出∠MON的度数即可;
(3)根据(2)中的结论,归纳总结表示出∠MON的度数即可.
解答: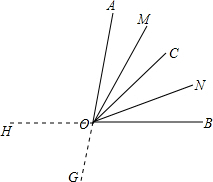 解:∵OM、ON分别平分∠AOC,∠BOC,
解:∵OM、ON分别平分∠AOC,∠BOC,
∴∠MOC=
∠AOC,∠NOC=
∠BOC,
(1)∠MON=∠MOC+∠NOC=
∠AOC+
∠BOC=
(∠AOC+∠BOC)=
∠AOB=40°;
(2)反向延长OA,OB到G,H,
分三种情况考虑:
(i)当OC落在∠AOH内时,可得∠MON=∠NOC=∠MOC=
∠BOC-
∠AOC=
(∠BOC-∠AOC)=
∠AOB=40°;
(ii)当OC落在∠BOG内时,可得∠MON=∠MOC-∠NOC=
∠AOC-
∠BOC=
(∠AOC-∠BOC)=
∠AOB=40°;
(iii)当OC落在∠HOG内时,可得∠MON=∠MOC+∠NOC=
∠AOC+
∠BOC=
(∠AOC+∠BOC)=
(360°-∠AOB)=140°,
综上,∠MON=40°或140°;
(3)归纳总结得:当∠AOB=α时,∠MON=
α或180°-
α.
 解:∵OM、ON分别平分∠AOC,∠BOC,
解:∵OM、ON分别平分∠AOC,∠BOC,∴∠MOC=
| 1 |
| 2 |
| 1 |
| 2 |
(1)∠MON=∠MOC+∠NOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)反向延长OA,OB到G,H,
分三种情况考虑:
(i)当OC落在∠AOH内时,可得∠MON=∠NOC=∠MOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(ii)当OC落在∠BOG内时,可得∠MON=∠MOC-∠NOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(iii)当OC落在∠HOG内时,可得∠MON=∠MOC+∠NOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
综上,∠MON=40°或140°;
(3)归纳总结得:当∠AOB=α时,∠MON=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了角的计算,以及角平分线,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
已知二次函数y=-x2-
x+1,当自变量x取m时,对应的函数值大于0,设自变量分别取m-3,m+3时对应的函数值为y1,y2,则下列判断正确的是( )
| 3 |
| 2 |
| A、y1<0,y2<0 |
| B、y1<0,y2>0 |
| C、y1>0,y2<0 |
| D、y1>0,y2>0 |
已知a、b互为相反数,c、d互为倒数,|x-1|=1,则代数式x2-(a+b-cd)x+(-cd)2013的值等于( )
| A、5 | B、1 |
| C、1或-1 | D、5或-1 |
 如图,长方形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx-2的图象,过点A和点C,并与y轴交于点E,则k=
如图,长方形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx-2的图象,过点A和点C,并与y轴交于点E,则k=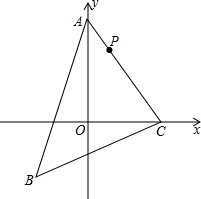 如图,已知△ABC三个顶点坐标分别为A(0,4),B(-2,-2),C(3,0),点P在线段AC上移动.当点P坐标为(1,m)时,请在y轴上找点Q,使△PQC周长最小.
如图,已知△ABC三个顶点坐标分别为A(0,4),B(-2,-2),C(3,0),点P在线段AC上移动.当点P坐标为(1,m)时,请在y轴上找点Q,使△PQC周长最小.