题目内容
8.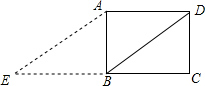 如图,已知矩形ABCD中,AB=3,BC=4,如果将线段BD绕着点B旋转后,点D落在CB的延长线的E处,则tanE=$\frac{3}{5}$.
如图,已知矩形ABCD中,AB=3,BC=4,如果将线段BD绕着点B旋转后,点D落在CB的延长线的E处,则tanE=$\frac{3}{5}$.
分析 首先由勾股定理求得BD=5,然后由旋转的性质可知BE=BD=5,然后利用正切函数的定义求解即可.
解答 解:∵四边形ABCD为矩形,
∴∠C=90°,AB∥DC.
在Rt△BCD中,$BD=\sqrt{B{C}^{2}+D{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
由旋转的性质可知EB=BD=5,
∵AB∥DC,
∴∠ABE=∠C=90°.
∴tanE=$\frac{AB}{BE}$=$\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 本题主要考查的是旋转的性质、矩形的性质以及勾股定理的应用,求得BE的长度是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.某次歌唱比赛,最后三名选手的成绩统计如表:
(1)若按算术平均分排出冠军、亚军、季军,则冠军、亚军、季军各是谁?
(2)若按6:3:1的加权平均分排出冠军、亚军、季军,则冠军、亚军、季军各是谁?
(3)若最后排名冠军是王晓丽,亚军是李真,季军是林飞扬,则权重可能是多少?
| 比赛项目 | 比赛成绩/分 | ||
| 王晓丽 | 李真 | 林飞扬 | |
| 唱功 | 98 | 95 | 80 |
| 音乐常识 | 80 | 90 | 100 |
| 综合知识 | 80 | 90 | 100 |
(2)若按6:3:1的加权平均分排出冠军、亚军、季军,则冠军、亚军、季军各是谁?
(3)若最后排名冠军是王晓丽,亚军是李真,季军是林飞扬,则权重可能是多少?
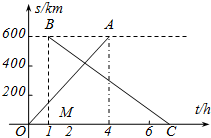 甲、乙两城市之间开通了动车组高速列车.已知每隔2h有一列速度相同的动车组列车从甲城开往乙城.如图,OA是第一列动车组列车离开甲城的路程s(km)与运行时间t(h)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(km)与运行时间t(h)的函数图象.请根据图中的信息,解答下列问题:
甲、乙两城市之间开通了动车组高速列车.已知每隔2h有一列速度相同的动车组列车从甲城开往乙城.如图,OA是第一列动车组列车离开甲城的路程s(km)与运行时间t(h)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(km)与运行时间t(h)的函数图象.请根据图中的信息,解答下列问题: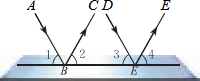 如图,一束平行光线AB与DE射向一个水平镜面而后被反射,此时∠1=∠2,∠3=∠4.反射光线BC与EF也平行吗?说明理由.
如图,一束平行光线AB与DE射向一个水平镜面而后被反射,此时∠1=∠2,∠3=∠4.反射光线BC与EF也平行吗?说明理由.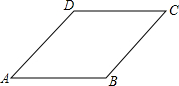 如图,已知菱形ABCD的边长为2,∠A=45°,将菱形ABCD绕点A旋转45°,得到菱形AB1C1D1,其中B、C、D的对应点分别是B1、C1、D1,那么点C、C1的距离为2$\sqrt{2}$.
如图,已知菱形ABCD的边长为2,∠A=45°,将菱形ABCD绕点A旋转45°,得到菱形AB1C1D1,其中B、C、D的对应点分别是B1、C1、D1,那么点C、C1的距离为2$\sqrt{2}$.