题目内容
17.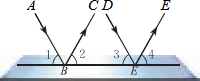 如图,一束平行光线AB与DE射向一个水平镜面而后被反射,此时∠1=∠2,∠3=∠4.反射光线BC与EF也平行吗?说明理由.
如图,一束平行光线AB与DE射向一个水平镜面而后被反射,此时∠1=∠2,∠3=∠4.反射光线BC与EF也平行吗?说明理由.
分析 由AB与DE平行,利用两直线平行同位角相等即可得到∠1=∠3,再由∠1=∠2,∠3=∠4,等量代换即可得到∠2=∠4,利用同位角相等两直线平行,即可得到BC与EF平行.
解答 解:平行,理由如下:
∵AB∥DE,
∴∠1=∠3,
又∵∠1=∠2,∠3=∠4,
∴∠2=∠4,
∴BC∥EF.
点评 此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
9.一组数据1,1,4,3,6的平均数和众数分别是( )
| A. | 1,3 | B. | 3,1 | C. | 3,3 | D. | 3,4 |
5.下列图形,既是轴对称图形,又是中心对称图形的是( )
| A. | 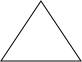 | B. | 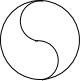 | C. |  | D. | 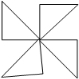 |
12.一个圆锥的底面半径为3,母线长为5,则圆锥的侧面积是( )
| A. | 9π | B. | 18π | C. | 15π | D. | 27π |
7.在Rt△ABC中,∠B=90°,AB=8,BC=6,将△ABC沿MN折叠(M、N分别在AC、AB上,且不与端点重合),使点A与BC上的点D重合,点D把线段BC分成长度之比是1:2的两条线段,则线段BN的长为( )
| A. | $\frac{15}{8}$ | B. | 3 | C. | 3或$\frac{15}{4}$ | D. | $\frac{15}{4}$或4 |
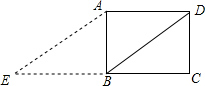 如图,已知矩形ABCD中,AB=3,BC=4,如果将线段BD绕着点B旋转后,点D落在CB的延长线的E处,则tanE=$\frac{3}{5}$.
如图,已知矩形ABCD中,AB=3,BC=4,如果将线段BD绕着点B旋转后,点D落在CB的延长线的E处,则tanE=$\frac{3}{5}$.