题目内容
18.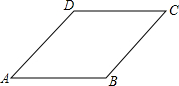 如图,已知菱形ABCD的边长为2,∠A=45°,将菱形ABCD绕点A旋转45°,得到菱形AB1C1D1,其中B、C、D的对应点分别是B1、C1、D1,那么点C、C1的距离为2$\sqrt{2}$.
如图,已知菱形ABCD的边长为2,∠A=45°,将菱形ABCD绕点A旋转45°,得到菱形AB1C1D1,其中B、C、D的对应点分别是B1、C1、D1,那么点C、C1的距离为2$\sqrt{2}$.
分析 首先由菱形的性质可知∠ABC=∠ADC=135°,由旋转的性质可知:∠AB′C′=135°,从而可证明△C′DC为直角三角形,然后由勾股定理即可求得C′C的长度.
解答 解:如图所示: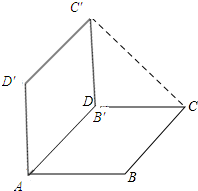
∵四边形ABCD为菱形,∠A=45°,
∴∠ABC=∠ADC=135°.
由旋转的性质可知:∠AB′C′=135°,B′C′=BC=2,
∴∠C′DC=360°-135°-135°=90°.
在Rt△C′DC中,C′C=$\sqrt{C′{B}^{2}+D{C}^{2}}$=$\sqrt{{2}^{2}+{2}^{2}}=2\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题主要考查的是旋转的性质和菱形的性质以及勾股定理的应用,证得△C′DC为直角三角形是解题的关键.

练习册系列答案
相关题目
7.在Rt△ABC中,∠B=90°,AB=8,BC=6,将△ABC沿MN折叠(M、N分别在AC、AB上,且不与端点重合),使点A与BC上的点D重合,点D把线段BC分成长度之比是1:2的两条线段,则线段BN的长为( )
| A. | $\frac{15}{8}$ | B. | 3 | C. | 3或$\frac{15}{4}$ | D. | $\frac{15}{4}$或4 |
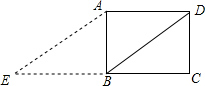 如图,已知矩形ABCD中,AB=3,BC=4,如果将线段BD绕着点B旋转后,点D落在CB的延长线的E处,则tanE=$\frac{3}{5}$.
如图,已知矩形ABCD中,AB=3,BC=4,如果将线段BD绕着点B旋转后,点D落在CB的延长线的E处,则tanE=$\frac{3}{5}$.