题目内容
1.现正是闽北特产杨梅热销的季节,某水果零售商店分两批次从批发市场共购进杨梅40箱,已知第一、二次进货价分别为每箱50元、40元,且第二次比第一次多付款700元.(1)设第一、二次购进杨梅的箱数分别为a箱、b箱,求a,b的值;
(2)若商店对这40箱杨梅先按每箱60元销售了x箱,其余的按每箱35元全部售完.
①求商店销售完全部杨梅所获利润y(元)与x(箱)之间的函数关系式;
②当x的值至少为多少时,商店才不会亏本.
(注:按整箱出售,利润=销售总收入-进货总成本)
分析 (1)根据题意得出a、b的方程组,解方程组即可;
(2)①根据利润=销售总收入-进货总成本,即可得出结果;
②商店要不亏本,则y≥0,得出不等式,解不等式即可.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{a+b=40}\\{40b-50a=700}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=10}\\{b=30}\end{array}\right.$;
答:a,b的值分别为10,30;
(2)①根据题意得:y=60x+35(40-x)-(10×50+30×40),
∴y=25x-300;
②商店要不亏本,则y≥0,
∴25x-300≥0,
解得:x≥12;
答:当x的值至少为12时,商店才不会亏本.
点评 本题考查了二元一次方程组的应用、一次函数的应用;根据题意得出等量关系列出方程组或得出函数关系式或由不等关系得出不等式是解决问题的关键.

练习册系列答案
相关题目
9.一组数据1,1,4,3,6的平均数和众数分别是( )
| A. | 1,3 | B. | 3,1 | C. | 3,3 | D. | 3,4 |
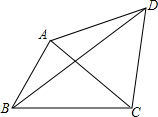 如图,在△ABC中,AB=2,BC=3,∠ABC=60°,△ACD是等边三角形,连接BD,则线段BD的长为$\sqrt{19}$.
如图,在△ABC中,AB=2,BC=3,∠ABC=60°,△ACD是等边三角形,连接BD,则线段BD的长为$\sqrt{19}$.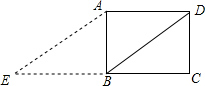 如图,已知矩形ABCD中,AB=3,BC=4,如果将线段BD绕着点B旋转后,点D落在CB的延长线的E处,则tanE=$\frac{3}{5}$.
如图,已知矩形ABCD中,AB=3,BC=4,如果将线段BD绕着点B旋转后,点D落在CB的延长线的E处,则tanE=$\frac{3}{5}$.