题目内容
18.已知一函数y=kx+3和y=-kx+2.则两个一次函数图象的交点在( )| A. | 第一、二象限 | B. | 第二、三象限 | C. | 三、四象限 | D. | 一、四象限 |
分析 联立方程组求得$\left\{\begin{array}{l}{x=-\frac{1}{2k}}\\{y=\frac{5}{2}}\end{array}\right.$,再分k>0和k<0分别讨论可得.
解答 解:由$\left\{\begin{array}{l}{y=kx+3}\\{y=-kx+2}\end{array}\right.$可得$\left\{\begin{array}{l}{x=-\frac{1}{2k}}\\{y=\frac{5}{2}}\end{array}\right.$,
当k>0时,交点的横坐标为负,纵坐标为正,即交点在第二象限;
当k<0时,交点的横坐标为正,纵坐标为正,即交点在第一象限;
故选:A.
点评 本题主要考查两直线相交或平行的问题及象限内点的坐标特点,掌握根据直线解析式求得交点坐标且各象限内点的坐标特点是解题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
13.下列图形中既是中心对称图形又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
3.某企业去年产值p万元,今年比去年增产10%,今年产值是( )
| A. | p(1+10%)万元 | B. | (p+10%)万元 | C. | $\frac{p}{1+10%}$万元 | D. | $\frac{p}{1-10%}$万元 |
10.已知射线OC在∠AOB的内部,下列关系式
①∠AOC=∠BOC;②∠AOC+∠BOC=∠AOB;③∠AOB=2∠AOC;④∠BOC=$\frac{1}{2}$∠AOB.其中,能说明OC为∠AOB的平分线的有( )
①∠AOC=∠BOC;②∠AOC+∠BOC=∠AOB;③∠AOB=2∠AOC;④∠BOC=$\frac{1}{2}$∠AOB.其中,能说明OC为∠AOB的平分线的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.已知三角形三边长分别为2,x,5,若x为整数,则这样的三角形个数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
8.在抛物线y=-2(x-1)2上的一个点是( )
| A. | (2,3) | B. | (-2,3) | C. | (1,-5) | D. | (0,-2) |
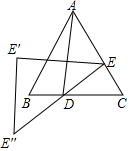 如图,在等边△ABC中,AB=4,D是BC边上任意一点(不与B,C重合),过点D作DE⊥AC,垂足为E,作点E关于直线AD对称的点E',作点E关于点D的对称点E″,作△EE'E″,当△EE'E″是轴对称图形时,S△EE'E″=48-24$\sqrt{3}$.
如图,在等边△ABC中,AB=4,D是BC边上任意一点(不与B,C重合),过点D作DE⊥AC,垂足为E,作点E关于直线AD对称的点E',作点E关于点D的对称点E″,作△EE'E″,当△EE'E″是轴对称图形时,S△EE'E″=48-24$\sqrt{3}$.