题目内容
6.若y=2$\sqrt{x-2}$+$\sqrt{2-x}$+$\frac{1}{3}$,则$\sqrt{x}$+$\sqrt{y}$=$\sqrt{2}$+$\frac{\sqrt{3}}{3}$.分析 直接利用二次根式的性质得出x的值,再得出y的值,进而求出答案.
解答 解:∵$\sqrt{x-2}$和$\sqrt{2-x}$都有意义,
∴x=2,
∴y=$\frac{1}{3}$,
故$\sqrt{x}$+$\sqrt{y}$=$\sqrt{2}$+$\sqrt{\frac{1}{3}}$=$\sqrt{2}$+$\frac{\sqrt{3}}{3}$.
故答案为:$\sqrt{2}$+$\frac{\sqrt{3}}{3}$.
点评 此题主要考查了二次根式有意义的条件,正确得出x,y的值是解题关键.

练习册系列答案
相关题目
16. 如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为$\frac{1000}{3}$π cm2,则扇形圆心角的度数为( )
如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为$\frac{1000}{3}$π cm2,则扇形圆心角的度数为( )
 如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为$\frac{1000}{3}$π cm2,则扇形圆心角的度数为( )
如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为$\frac{1000}{3}$π cm2,则扇形圆心角的度数为( )| A. | 120° | B. | 140° | C. | 150° | D. | 160° |
17.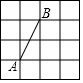 如图4×4的正方形网格中,网格线的交点叫格点,已知点A、B是格点,若C也是格点且△ABC为等腰三角形,则点C的个数是( )
如图4×4的正方形网格中,网格线的交点叫格点,已知点A、B是格点,若C也是格点且△ABC为等腰三角形,则点C的个数是( )
 如图4×4的正方形网格中,网格线的交点叫格点,已知点A、B是格点,若C也是格点且△ABC为等腰三角形,则点C的个数是( )
如图4×4的正方形网格中,网格线的交点叫格点,已知点A、B是格点,若C也是格点且△ABC为等腰三角形,则点C的个数是( )| A. | 6个 | B. | 7个 | C. | 8个 | D. | 9个 |
18.已知一函数y=kx+3和y=-kx+2.则两个一次函数图象的交点在( )
| A. | 第一、二象限 | B. | 第二、三象限 | C. | 三、四象限 | D. | 一、四象限 |
15.关于线段的垂直平分线有以下说法:①一条线段的垂直平分线的垂足,也是这条线段的中点.②线段的垂直平分线是一条直线.③一条线段的垂直平分线就是这条线段的对称轴.其中正确的说法( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 无 |
16.下列y关于x的二次函数y=nx2-2x-n(n>0)的图象与x轴的交点的判断中,正确的是( )
| A. | 没有交点 | |
| B. | 只有一个交点,在x轴的负半轴上 | |
| C. | 有两个交点,都在x轴的正半轴 | |
| D. | 有两个交点,分别在x轴的正、负半轴上 |
 有理数a、b在数轴上的对应的位置如图所示,则下列各式①a+b<0;②a-b>0;③ab>0;④|a|>b;⑤1-b>0;⑥a+1>0,一定成立的有( )
有理数a、b在数轴上的对应的位置如图所示,则下列各式①a+b<0;②a-b>0;③ab>0;④|a|>b;⑤1-b>0;⑥a+1>0,一定成立的有( )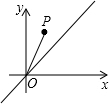 如图,在平面直角坐标系中,点P的坐标为(1,2),将线段OP沿y轴正方向移动m(m>0)个单位长度至O′P′,以O′P′为直角边在第一象限内作等腰直角△O′P′Q,若点Q在直线y=x上,则m的值为2或3.
如图,在平面直角坐标系中,点P的坐标为(1,2),将线段OP沿y轴正方向移动m(m>0)个单位长度至O′P′,以O′P′为直角边在第一象限内作等腰直角△O′P′Q,若点Q在直线y=x上,则m的值为2或3.