题目内容
4. 如图,矩形OABC放置在平面直角坐标系中,OA所在直线为x轴,OC所在直线为y轴,且OA=4,OC=2.当直线y=-x+b(0≤b≤6)中的b从0开始逐渐变大时,在矩形上扫过的面积记为S,则S关于b的函数图象是( )
如图,矩形OABC放置在平面直角坐标系中,OA所在直线为x轴,OC所在直线为y轴,且OA=4,OC=2.当直线y=-x+b(0≤b≤6)中的b从0开始逐渐变大时,在矩形上扫过的面积记为S,则S关于b的函数图象是( )| A. | 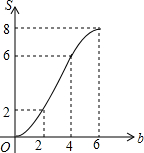 | B. |  | C. | 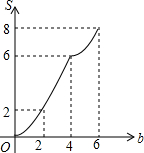 | D. | 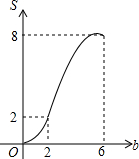 |
分析 当0≤b≤4;4≤b<8;b≥8时,分别求出S,然后根据求得的解析式得到对应的函数图象即可找到正确选项.
解答 解:①当0≤b≤2,S=$\frac{1}{2}$•b2;
它的函数图象为抛物线的一部分,开口向上;
②当2≤b<4,S=(b-2)×2+$\frac{1}{2}×2×2$=2b-2,
它的函数图象为一次函数的一部分,S随b的增大而增大,
③当b≥4,S=8-$\frac{1}{2}$(4-b)2=-$\frac{1}{2}$(b-4)2+8,;
它的函数图象为抛物线的一部分,开口向下;
所以B选项正确.
故选B.
点评 本题考查了运用分类的思想求动点的函数图象的问题:分别求出每个时段的函数关系式,然后根据自变量和函数解析式作出相应的图象.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
10.下列各组数中,数值相等的是( )
| A. | 32和23 | B. | -32和(-3)2 | C. | (-2)3和-23 | D. | -(-2)和-|-2| |
9.下列计算正确的是( )
| A. | 3a-(2a-c)=3a-2a+c | B. | 3a+2(2b-3c)=3a+4b-3c | ||
| C. | 6a+(-2b+5)=6a+2b-5 | D. | (5x-3y)-(2x-y)=5x+3y-2x+y |
 如图,抛物线y=$\frac{1}{4}$x2-$\frac{1}{2}$x-2与x轴交于A、B两点,与y轴交于点C,过点A的直线y=x+2交y轴于D,交抛物线于P点.
如图,抛物线y=$\frac{1}{4}$x2-$\frac{1}{2}$x-2与x轴交于A、B两点,与y轴交于点C,过点A的直线y=x+2交y轴于D,交抛物线于P点. 如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,点P是线段AC上的一动点,过点P作PQ∥AB交BC于点Q.设AP=x,S△PCQ=y,则y关于x的函数图象大致是( )
如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,点P是线段AC上的一动点,过点P作PQ∥AB交BC于点Q.设AP=x,S△PCQ=y,则y关于x的函数图象大致是( )