题目内容
15. 如图,抛物线y=$\frac{1}{4}$x2-$\frac{1}{2}$x-2与x轴交于A、B两点,与y轴交于点C,过点A的直线y=x+2交y轴于D,交抛物线于P点.
如图,抛物线y=$\frac{1}{4}$x2-$\frac{1}{2}$x-2与x轴交于A、B两点,与y轴交于点C,过点A的直线y=x+2交y轴于D,交抛物线于P点.(1)求点D的坐标;
(2)求△PAC的外接圆的直径长.
分析 (1)令x=0,求得直线y=x+2交y轴的交点D;
(2)求得抛物线y=$\frac{1}{4}$x2-$\frac{1}{2}$x-2与y轴的交点C,进一步把抛物线y=$\frac{1}{4}$x2-$\frac{1}{2}$x-2与直线y=x+2联立方程组求得A、P两点的坐标,利用勾股定理求得AP、AC、PC,根据勾股定理逆定理判定△PAC的形状,进一步求得外接圆的直径长即可.
解答 解:(1)令x=0,则y=x+2=2,
则点D坐标为(0,2);
(2)令x=0,则抛物线y=$\frac{1}{4}$x2-$\frac{1}{2}$x-2与y轴的交点C为(0,-2),
由题意得$\left\{\begin{array}{l}{y=\frac{1}{4}{x}^{2}-\frac{1}{2}x-2}\\{y=x+2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=-2}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=8}\\{y=10}\end{array}\right.$,
因此点A坐标为(-2,0),P点的坐标为(8,10),
则AC=$\sqrt{4+4}$=2$\sqrt{2}$,AP=$\sqrt{1{0}^{2}+1{0}^{2}}$=10$\sqrt{2}$,PC=$\sqrt{{8}^{2}+1{2}^{2}}$=4$\sqrt{13}$,
∵AC2+AP2=8+200=208,PC2=208,
∴AC2+AP2=PC2,
∴△PAC为直角三角形,且PC为斜边,
∴△PAC的外接圆的直径长为4$\sqrt{13}$.
点评 此题考查抛物线与x轴的交点,勾股定理、勾股定理逆定理的运用,三角形的外交圆的性质,求得△PAC三个顶点坐标,求得三边长是解决问题的关键.

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |

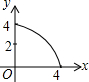
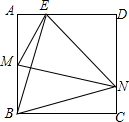 如图,四边形ABCD为正方形,若AB=4,E是AD边上一点(点E与点A、D不重合),BE的中垂线交AB于点M,交DC于点N,设AE=x,BM=y,则y与x的大致图象是( )
如图,四边形ABCD为正方形,若AB=4,E是AD边上一点(点E与点A、D不重合),BE的中垂线交AB于点M,交DC于点N,设AE=x,BM=y,则y与x的大致图象是( )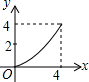
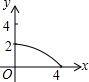
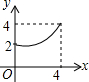
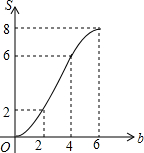
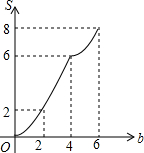
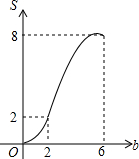
 如图,矩形OABC放置在平面直角坐标系中,OA所在直线为x轴,OC所在直线为y轴,且OA=4,OC=2.当直线y=-x+b(0≤b≤6)中的b从0开始逐渐变大时,在矩形上扫过的面积记为S,则S关于b的函数图象是( )
如图,矩形OABC放置在平面直角坐标系中,OA所在直线为x轴,OC所在直线为y轴,且OA=4,OC=2.当直线y=-x+b(0≤b≤6)中的b从0开始逐渐变大时,在矩形上扫过的面积记为S,则S关于b的函数图象是( )