题目内容
19. 如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,点P是线段AC上的一动点,过点P作PQ∥AB交BC于点Q.设AP=x,S△PCQ=y,则y关于x的函数图象大致是( )
如图,在Rt△ABC中,∠C=90°,AC=2,BC=4,点P是线段AC上的一动点,过点P作PQ∥AB交BC于点Q.设AP=x,S△PCQ=y,则y关于x的函数图象大致是( )| A. |  | B. |  | C. |  | D. | 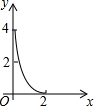 |
分析 由已知条件得到PC=2-x,通过△PCQ∽△ACB,根据相似三角形的性质得到$\frac{PC}{AC}=\frac{CQ}{BC}$,求得CQ=4-2x,由三角形的面积公式即可得到结论.
解答 解:∵AC=2,AP=x,
∴PC=2-x,
∵PQ∥AB,
∴△PCQ∽△ACB,
∴$\frac{PC}{AC}=\frac{CQ}{BC}$,
即:$\frac{2-x}{2}=\frac{CQ}{4}$,
∴CQ=4-2x,
∴y=$\frac{1}{2}$(2-x)(4-2x)=(x-2)2,
故选D.
点评 本题考查了动点问题的函数图象,相似三角形的判定和性质,根据相似三角形的性质求得QC是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.若(x-2)0-(x-3)-4有意义,那么x的取值范围是( )
| A. | x>2 | B. | x>3 | C. | x≠2或x≠3 | D. | x≠2且x≠3 |
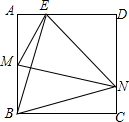 如图,四边形ABCD为正方形,若AB=4,E是AD边上一点(点E与点A、D不重合),BE的中垂线交AB于点M,交DC于点N,设AE=x,BM=y,则y与x的大致图象是( )
如图,四边形ABCD为正方形,若AB=4,E是AD边上一点(点E与点A、D不重合),BE的中垂线交AB于点M,交DC于点N,设AE=x,BM=y,则y与x的大致图象是( )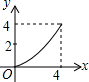
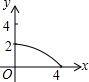
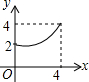
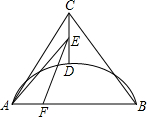 如图,AC=BC,点D是以线段AB为弦的圆弧的中点,AB=4,点E、F分别是线段CD,AB上的动点.设AF=x,AE2-FE2=y,则能表示y与x的函数关系的图象是( )
如图,AC=BC,点D是以线段AB为弦的圆弧的中点,AB=4,点E、F分别是线段CD,AB上的动点.设AF=x,AE2-FE2=y,则能表示y与x的函数关系的图象是( )
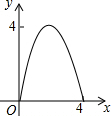
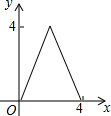
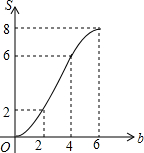
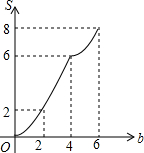
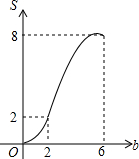
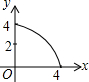
 如图,矩形OABC放置在平面直角坐标系中,OA所在直线为x轴,OC所在直线为y轴,且OA=4,OC=2.当直线y=-x+b(0≤b≤6)中的b从0开始逐渐变大时,在矩形上扫过的面积记为S,则S关于b的函数图象是( )
如图,矩形OABC放置在平面直角坐标系中,OA所在直线为x轴,OC所在直线为y轴,且OA=4,OC=2.当直线y=-x+b(0≤b≤6)中的b从0开始逐渐变大时,在矩形上扫过的面积记为S,则S关于b的函数图象是( )